Bindow 六月记事本
As Usual
一切如常,最近爱听Jazz,但并不能平静。
希望有打动我的东西,或者人,但都不会出现。
Way too damn needy.
又想起And You don’t Remember时期的Struggle&Pains,但是还是想重温这种感觉。
太平静了,却又酝酿着阴郁和刺耳,
到这便停吧。
好玩的事儿
看到很多有趣的事情,和有趣的人。
毕竟生活是要朝好的方向发展,
好听的话是要说的。
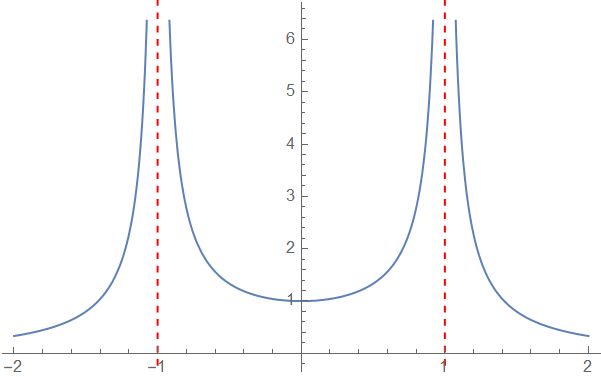
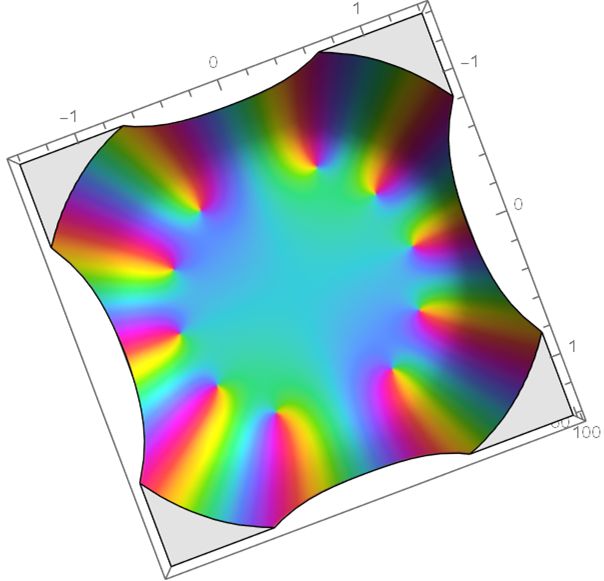
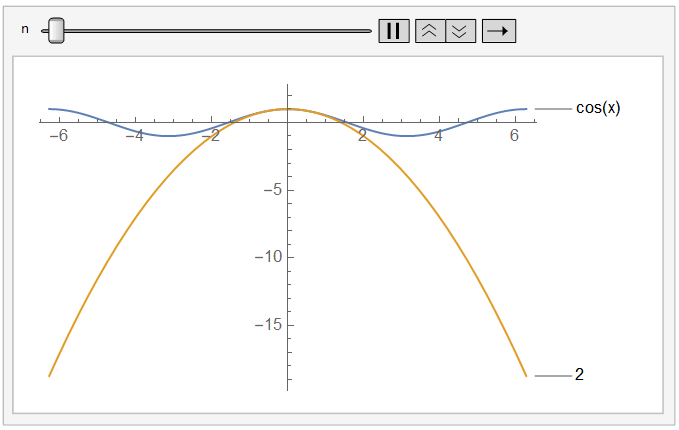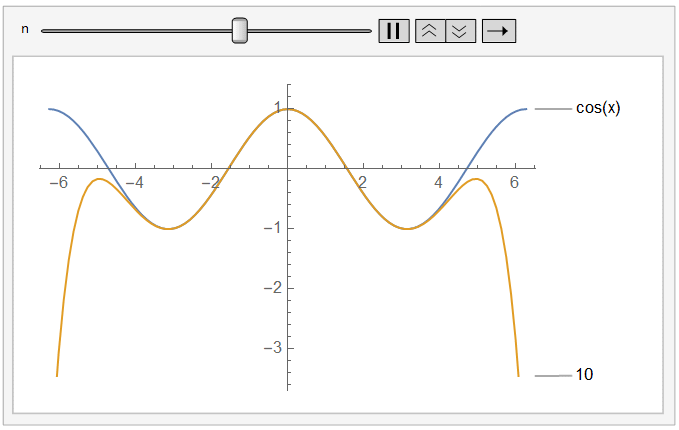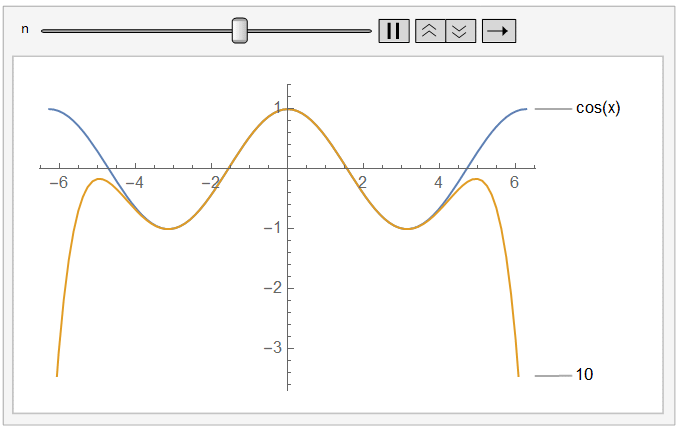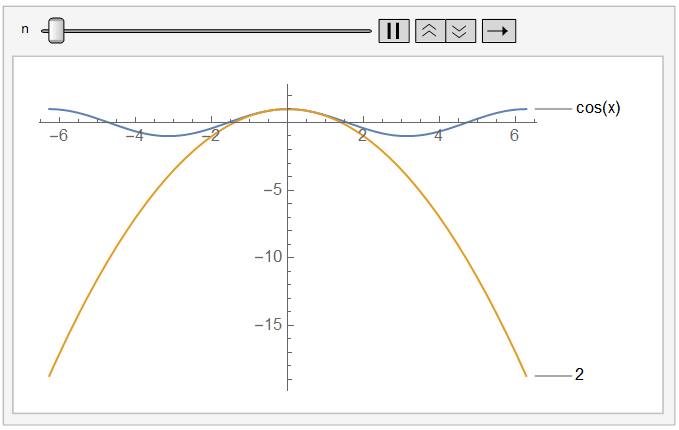
复分析真的好神奇
我居然爱上课后习题,真是绝无仅有。
[……]