实多项式的分解
简单的因式分解是中学的内容,其推广在高等代数中有详细展开。我们知道,有些实多项式在实数域上是不可被分解的,例如x^2+1就是如此。
一类多项式的分解
考虑一类实多项式x^n-1在实数域上的分解,对于n=1,2,3,4的情况我们有:
\begin{array}{l}
U_{1}(x)= x-1 \\
U_{2}(x)=(x-1)(x+1) \\
U_{3}(x)=(x-1)\left(x^{2}+x+1\right) \\
U_{4}(x)=(x-1)(x+1)\left(x^{2}+1\right)
\end{array}这样的模式对前几个多项式可能容易推导,但当n足够大时,很难寻找一个合适的模式来确定其分解。
尝试
对于最简单的情况U_2(x)而言(U_1(x)是不可约多项式),使用最简单的几何工具,我们可以构造如下的图形:
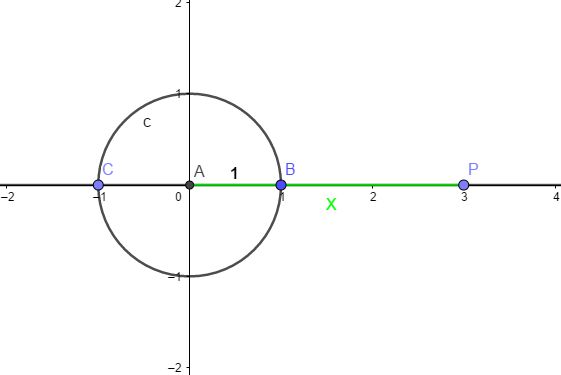
其中P为数轴上任意一点,OP的距离为x, AB为该单位圆的一个半径,长度为1.
那么我们有:
U_2(x)=PB\cdot PC=(x-1)(x+1)
到目前为止, 似乎单位圆的存在仅仅是为了构造一个1而已, 但仔细考虑, 对U_4(x)来说
U_4(x)=U_2(x)\cdot (x^2+1)=U_2(x)\cdot \sqrt{x^2+1}\cdot \sqrt{x^2+1}对这种模式很敏感的我们应该联想到勾股定理,并作出如下图:
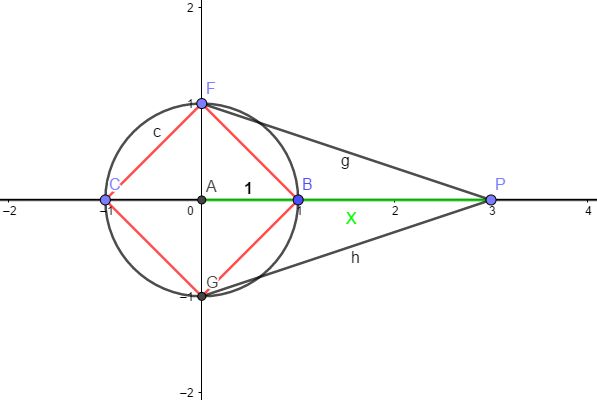
其中很显然的, FP=GP=\sqrt{x^2+1},
那么
U_4(x)=BP\cdot CP\cdot FP\cdot GP = (x-1)(x+1)(x^{2}+1)这种模式是否可以在其他几个多项式上成立?
测试这种几何模式
我们对第三个多项式进行测试, 按照这种模式, 圆内应有一个内接正三角形, 如下图:
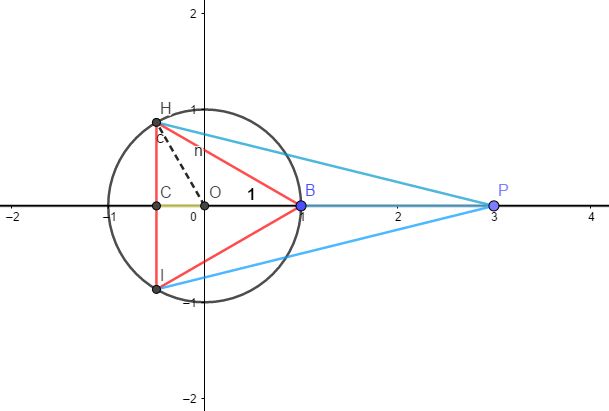
其中CO=\frac{1}{2}, CH=\frac{\sqrt{3}}{2}, 那么HP=IP=[(x+\frac{1}{2})^2+(\frac{\sqrt{3}}{2})^2], 所以
U_3(x)=BP\cdot HP^2=(x-1)(x^2+x+1)
Match!
那我们有足够的理由推断对于U_n(x)而言, 需要一个内接正n边形, 即
<blockquote><p>若<code class="katex-inline">C_1C_2C_3···C_n</code>时内接于以<code class="katex-inline">O</code>为中心的单位圆的正<code class="katex-inline">n</code>边形, <code class="katex-inline">P</code>是直线<code class="katex-inline">OC_1</code>上与<code class="katex-inline">O</code>的距离为<code class="katex-inline">x</code>的一点, 则</p><pre><code class="language-katex">U_n(x)=PC_1\cdot PC_2\cdot PC_3···PC_n</code></pre></blockquote>
但我们该如何证明它呢?
复平面与复数
考虑一个n=12的情况, 我们有如下图所示的单位圆与正多边形:
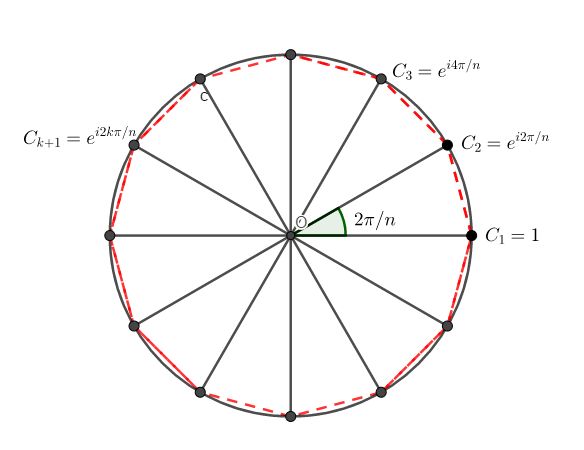
第k+1个顶点就是C_{k+1}=e^{ik(2\pi /n)},k=0,1,···,n-1.
那么我们发现, 正n边形的n个顶点正是U_n(z)=z^n-1的n个复根.
那么(z^n)-1的完全因式分解为z^n-1=U_n(z)=(z-C_1)(z-C_2)···(z-C_n),
每一对共轭根给出一个实二次因式:
(z-e^{ik(2\pi /n)})(z^e{-ik(2\pi /n)})=z^2-2z\cos [\frac{2k\pi}{n}]+1例如, 对于正12边形的情况, 当k=2时, 有1-x+x^2.
而在这个例子中,我们有5对共轭根和两个单独的复根(分别是第0个与第6个),所以在实数域上分解出的因式应该有7个因子。
最后我们通过因式分解得到的实多项式为
(x-1) (x+1) \left(x^2+1\right) \left(x^2-x+1\right) \left(x^2+x+1\right) \left(x^2-\sqrt{3} x+1\right) \left(x^2+\sqrt{3} x+1\right)正好有7个因式。
Reference
Viusal Complex Analysis
