重新发明复数 —— 篇一三次方程和复数

从三次方程说起

对于一个一般的三次方程 $x^3=3px+2q$ , 我们可以证明他必定有解。

通过卡丹诺的推导我们可以得到通解的形式(要得到有意义的解需满足: $q^2\ge p^3$ )：

 $x=\sqrt[3]{q+\sqrt{q^{2}-p^{3}}}+\sqrt[3]{q-\sqrt{q^{2}-p^{3}}}$

例如例子 $x^3=6x+6$ ,由上面的通解形式很容易得到解为 $2^{1/3}+2^{2/3}\approx2.84732$ .

而对于这样一个例子

 $x^3=15x+4$

我们有

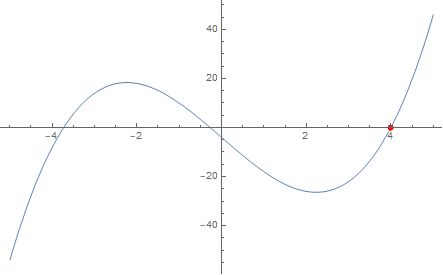
 $x=\sqrt[3]{2+11 i}+\sqrt[3]{2-11 i}$

目前我们无法知晓 $i$ 的存在到底会如何影响最终的解，但是由下图可以看出这个方程有一个解 $x=4$ (这里忽略掉剩下两个解).

很显然， $\sqrt[3]{2+11 i}+\sqrt[3]{2-11 i}=4$ , 但是我们并不知道有关 $i$ 的运算法则(当然我们还是知道 $i^2=-1$ )，注意到左式的两项中都有2，会不会是这两个2相加等于4呢？

如果我们假设 $\sqrt[3]{2+11 i}=2+n i$ , $\sqrt[3]{2-11 i}=2-n i$ , 对两式左右两边分别三次方运算，得到 $2+11i=(2+ni)^3$ , $2-11i=(2-ni)^3$ 。

我们希望对 $i$ 的运算满足结合律,即

 $(a+i \widetilde{a})(b+i \tilde{b})=a b+i(a \widetilde{b}+\widetilde{a} b)+i^{2} \widetilde{a} \tilde{b}$

而 $i^2=-1$ , 所以两个复数的乘积应该为

 $(a+i \widetilde{a})(b+i \widetilde{b})=(a b-\widetilde{a} \tilde{b})+i(a \widetilde{b}+\widetilde{a} b)$

当然，复数的加法也可以很自然的服从交换律和结合律。

通过这种假定，我们可以得到

 $(2-11i)=(2-i)^3, (2+11i)=(2+i)^3$

而

 $2+i+2-i=4$

这样我们就以一个与实数运算类似的方法定义了复数的一些运算法则。

Visual Complex Analysis

浏览量: 40