复分析

从收敛区间到收敛圆

神敲开实数的墙，创造了无上的圆。

我们在上一篇文章中讨论了f(x)=\frac{1}{x^2-1}的收敛性，我们可以看到，对于|f(x)|来说(一般来说，加绝对值不会对收敛区间有改变)，其收敛区间与爆破点的紧密联系:

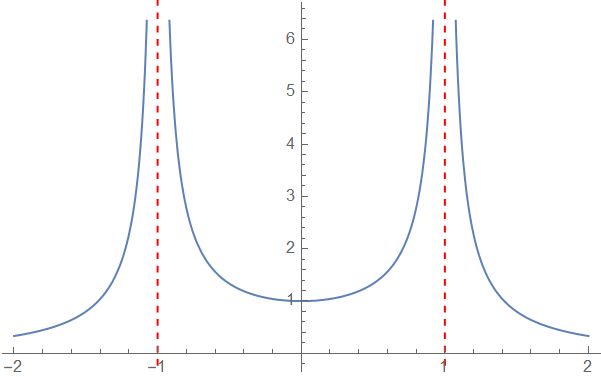
让我们在复数域上看看收敛区间是如何拓展的.

让我们直接对[……]

继续阅读

从一些例子引入收敛半径

I. 例子A

考虑一个多项式函数f(x)=\frac{1}{x-1}, 它的泰勒级数为\textbf{Series}(f)=1+x^2+x^3+···

再考虑一个三角函数g(x)=\cos(x)的泰勒级数\textbf{Series}(g)=1+\frac{x^2}{2!}+[......]

Prelude: Complex Function as Transformation

和高等代数相似地，将复数看作复平面上的线性变换，即z\mapsto w = f(z)=(a+bi)z,由复数的性质我们有下图(i将点列逆时针旋转90度)，此处不再赘述.

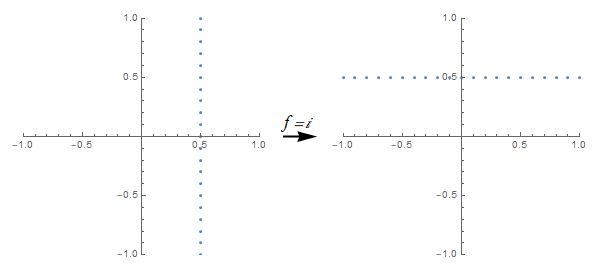
当然，我们使用r\theta也能得到一样[……]

继续阅读

从一个方程说起

考虑如下方程的在复数域解:

1=z^{3}

我们有:

z=1,z=(-1)^{2/3},z=-(-1)^{2/3}

乍一看来, 只有第一个解是可以立马得到的, 而剩下的两个解则需要一些运算。

如果遇到z_0=z^{n}这样的方程, 他有什么特质呢?

复数域上的变换

回到第一个方程,[……]

继续阅读

叉积与多边形面积

任意多边形的面积并不总是十分好求的，对于边数少的多边形或正多边形，我们由公式即可计算面积，但是对于复杂的多边形，并没有很直观的公式来计算面积。

对简单情况的描述

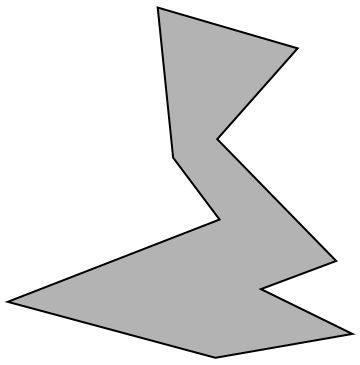
考虑一个简单的正四边形，边长为二的情况下，它的面积为4.

正方形的面积公式告诉我们它的面积可以简单地通过2\times[......]

实多项式的分解

简单的因式分解是中学的内容，其推广在高等代数中有详细展开。我们知道，有些实多项式在实数域上是不可被分解的，例如x^2+1就是如此。

一类多项式的分解

考虑一类实多项式x^n-1在实数域上的分解，对于n=1,2,3,4的情况我们有:

这样的模式对前几个多项式[……]

继续阅读

从三次方程说起

对于一个一般的三次方程x^3=3px+2q, 我们可以证明他必定有解。

通过卡丹诺的推导我们可以得到通解的形式(要得到有意义的解需满足:q^2\ge p^3)：

x=\sqrt[3]{q+\sqrt{q^{2}-p^{3}}}+\sqrt[3]{q-\sqrt{q^{2}-p^{3}[......]
继续阅读