Recent recapitulate of Real Analysis
不知為何，數學家總是和積分過不去。在大多數情況下，Riemann積分都是足夠使用的（更精確地說，每一個分段連續的(pairwise continuous)函數都是Riemann可積的），但分段連續的函數只是一類函數，對於Riemann不可積的函數，例如
我們需要建立一個更普適的積分概念來處[……]
数学
Lebesgue Measure approximation graph using Mathematica
Wolfram’s online code lab powers this article. Please click to see the demonstration on Lebsgue approximation of the given function.
[……]
Why do we need sigma algebras to define probability spaces?
A theory of probability admitting all subsets of UNCONOUNTABLE sets will break mathematics, but 𝝈-algebras are the patch that fixes math.[……]
傅里叶级数-周期函数的优雅表示
我们为什么需要傅里叶级数？
一种通常的想法是，对于一个周期函数（或非周期函数），使用傅里叶级数（或傅里叶变换），能够从时域（时间维度）转移到频域（频率维度），将复杂的周期（非周期）函数看作一个正交规范系下的一组基，从而更有效的进行分析与计算。
同时，这种做法可以有效的提取出函数中的有效信[……]
2021年数模国赛A题论文: FAST主动反射面的最优调整
2021年全国大学生数学建模竞赛A题国一论文，射电望远镜FAST主动反射面的最优调整。使用Mathematica进行代数建模，与评审要求高度接近。[……]
Mathematica How To II —— 数值全局最优化方法
Mathematica How To II —— 数值全局最优化方法
今天小编给大家介绍在Mathematica中如何进行数值全局最优化，我们都知道，在Mathematica中如何进行数值全局最优化需要使用NMinimize函数，那么Mathematica中如何进行数值全局最优化是什么呢？在Math[……]
重新发明复数 篇七 复数域上的收敛性下篇
从收敛区间到收敛圆
神敲开实数的墙，创造了无上的圆。
我们在上一篇文章中讨论了f(x)=\frac{1}{x^2-1}的收敛性，我们可以看到，对于|f(x)|来说(一般来说，加绝对值不会对收敛区间有改变)，其收敛区间与爆破点的紧密联系:
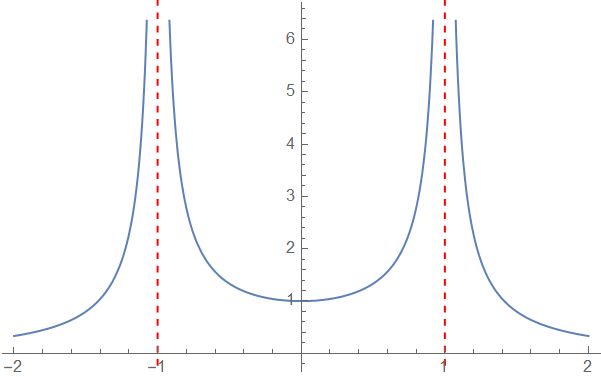
让我们在复数域上看看收敛区间是如何拓展的.
让我们直接对[……]
重新发明复数 篇六 复数域上的收敛性上篇
从一些例子引入收敛半径
I. 例子A
考虑一个多项式函数f(x)=\frac{1}{x-1}, 它的泰勒级数为\textbf{Series}(f)=1+x^2+x^3+···
再考虑一个三角函数g(x)=\cos(x)的泰勒级数\textbf{Series}(g)=1+\frac{x^2}{2!}+[......]
重新发明复数 篇五 卡西尼曲线和复数域上的变换
Prelude: Complex Function as Transformation
和高等代数相似地，将复数看作复平面上的线性变换，即z\mapsto w = f(z)=(a+bi)z,由复数的性质我们有下图(i将点列逆时针旋转90度)，此处不再赘述.
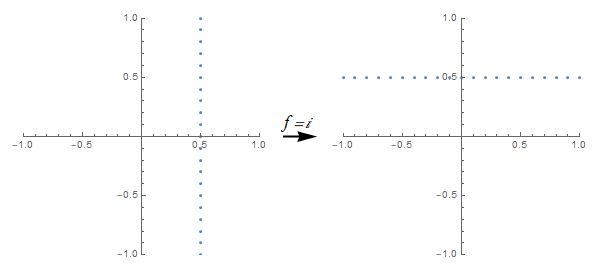
当然，我们使用r\theta也能得到一样[……]