Introduction to Julia Plot
Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated funciton values. Thus the behavior of the function on the Julia set is “chaotic”.
Let $R(z)$ be a rational fuction
$$R(z)\equiv \frac{P(z)}{Q(z)}$$
, where $z\in \mathbb{C}^*$, $\mathbb{C}^*$ is the Riemann sphere $\mathbb{C}\cup {\infty}$, and $P$ and $Q$ are ploynomials without common divisors. The Julia set $J_R$ is the set of points $z$ which do not approach infinity after $R(z)$ is repeatly applied.
Quadratic Julia sets are generated by the quadratic mapping
$$z_{n+1}=z_n^2+c$$
for fixed $c$. For almost every $c$, this transformation generates a fractal.
CUDALink and its code
CUDALink allows the Wolfram Language to use the CUDA parallel computing architecture on Graphical Processing Units (GPUs). It contains functions that use CUDA-enabled GPUs to boost performance in a number of areas, such as linear algebra, financial simulation, and image processing. CUDALink also integrates CUDA with existing Wolfram Language development tools, allowing a high degree of automation and control.
__global __ void julia_kernel(Real_t * set, mint width, mint height, \
Real_t cx, Real_t cy) {
int xIndex = threadIdx.x + blockIdx.x*blockDim.x;
int yIndex = threadIdx.y + blockIdx.y*blockDim.y;
int ii;
Real_t x = ZOOM_LEVEL*(width/2 - xIndex);
Real_t y = ZOOM_LEVEL*(height/2 - yIndex);
Real_t tmp;
Real_t c;
if (xIndex < width && yIndex < height) {
for (ii = 0; ii < MAX_ITERATIONS && sqrtf((x*x - y*y + \
cx)*(x*x-y*y+cx)+(2*x*y+cy)*(2*x*y+cy))< BAILOUT; ii++) {
tmp = x*x - y*y + cx;
y = 2*x*y + cy;
x = tmp;
}
c = logf(sqrtf((x*x - y*y + cx)*(x*x-y*y+cx)+(2*x*y+cy)*(2*x*y+cy)));
set[xIndex + yIndex*width] = c;
}
}This allows to generate new matrix every user-input c. Using Manipulate and Locator, a danamic plot can be achieved.
{width, height} = {512, 512};
jset = CUDAMemoryAllocate[Real, {height, width}];
JuliaCalculate =
CUDAFunctionLoad[code,
"julia_kernel", {{_Real, _,
"Output"}, _Integer, _Integer, _Real, _Real}, {16, 16},
"Defines" -> {"MAX_ITERATIONS" -> 1000, "ZOOM_LEVEL" -> "0.01",
"BAILOUT" -> "1024.0"}];
Manipulate[
JuliaCalculate[jset, width, height, c[[1]],
c[[2]], {width, height}];
ReliefPlot[Abs@CUDAMemoryGet[jset],
DataRange -> {{-2.0, 2.0}, {-2.0, 2.0}}, ImageSize -> 512,
ColorFunction -> "Rainbow"],
{{c, {0, 1}}, {-2, -2}, {2, 2}, Locator}]Manipulate[
JuliaCalculate[jset, width, height, c[[1]],
c[[2]], {width, height}];
ReliefPlot[Abs@CUDAMemoryGet[jset],
DataRange -> {{-2.0, 2.0}, {-2.0, 2.0}}, ImageSize -> 512,
ColorFunction -> "Rainbow"],
{{c, {0, 1}}, {-2, -2}, {2, 2}, Locator}]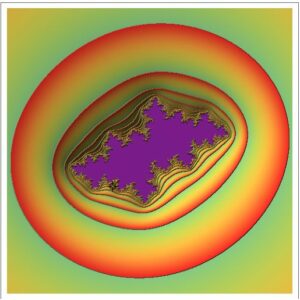

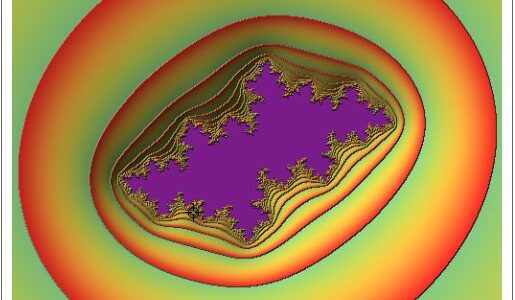
Really good. Hi, nice to meet you. I’m Tan Qiancheng, I think your code is so cool, thank you.