第二章——信息的表示和处理
整数表示
整型数据类型
long是唯一一个与机器相关的大小指示符. 它在32位机器上是4字节的, 在64位机器上是8字节的.
无符号数的编码
原理: 无符号数编码的定义
对向量\overrightarrow{x}=[x_{w-1},x_{w-2},...,x_0]:
B2U_w(\overrightarrow{x}) \dot{=} \sum^{w-1}_{i=0}{x_i2^i}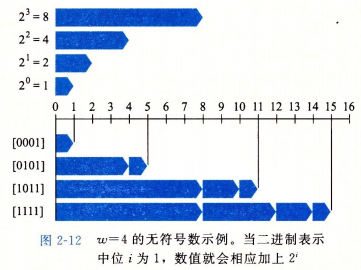
补码编码
原理: 补码编码的定义
对向量\overrightarrow{x}=[x_{w-1},x_{w-2},...,x_0]
有:
B2T_w(\overrightarrow{x}) \dot{=} -x_{w-1}2^{w-1}+\sum^{w-2}_{i=0}{x_i2^i})
有符号数的其他表示方法
- 反码(Ones’ Complement):
除了最高有效位的权是-(2^{w-1}-1)而不是-2^{w-1}, 它和补码是一样的:
B2O_w(\overrightarrow{x}) \dot{=}-x_{w-1}(2^{w-1}-1)+\sum_{i=0}^{w-2}x_i2^i- 原码(Sign-Manitude):
最高有效位是符号位, 用来决定剩下的为应该取负权还是正权:
B2S_w(\overrightarrow{x}) \dot{=} (-1)^x_{w-1} \cdot (\sum_{i=0}^{w=2}x_i2^i)
有符号数和无符号数之间的转换


C语言中的有符号数与无符号数
当执行一个运算时, 如果他的一个运算符是由富豪的而另一个是无符号的, 那么C语言会将有符号数隐式强转为无符号数.
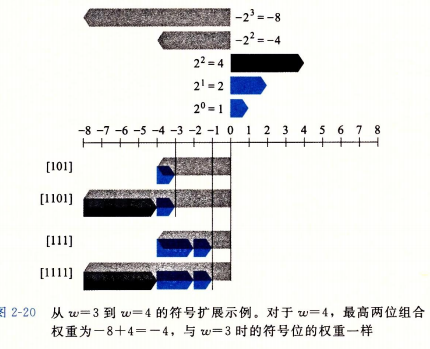
拓展一个数字的位表示
要将一个无符号数转换为一个更大的数据类型, 我们只要简单的在表示的开头添加0. 这种运算被称为零拓展(Zero extension).
截断数字
原理: 截断无符号数
令\overrightarrow{x}等于位向量[x_{w-1},x_{w-1},...,x_0],
而\overrightarrow{x}'是将其截断位k位的结果: \overrightarrow{x}'=[x_{k-1},x_{k-2},...,x_0].
令x=B2U_w(\overrightarrow{x}),x'=B2U_k(\overrightarrow{x}').
则x'=x\space\mathsf{mod}\space2^k
原理: 截断补码数
其实就是把二进制数按照截断无符号数的方法再进行补码转换.

慢慢来
加油