2021年全国大学生数学建模竞赛A题国一论文（2021A），射电望远镜FAST主动反射面的最优调整。使用Mathematica进行建模。

Written by Bindow. Copyright. https://www.bindow.top

2021A问题介绍

这个问题是2021数模国赛CUMCM中的问题A，讨论的是贵州天眼FAST主动反射面的调节和优化，问题的主干部分如下：

FAST 由主动反射面、信号接收系统（馈源舱）以及相关的控制、测量和支承系统组成（如图 1 所示），其中主动反射面系统是由主索网、反射面板、下拉索、促动器及支承结构等主要部件构成的一个可调节球面。

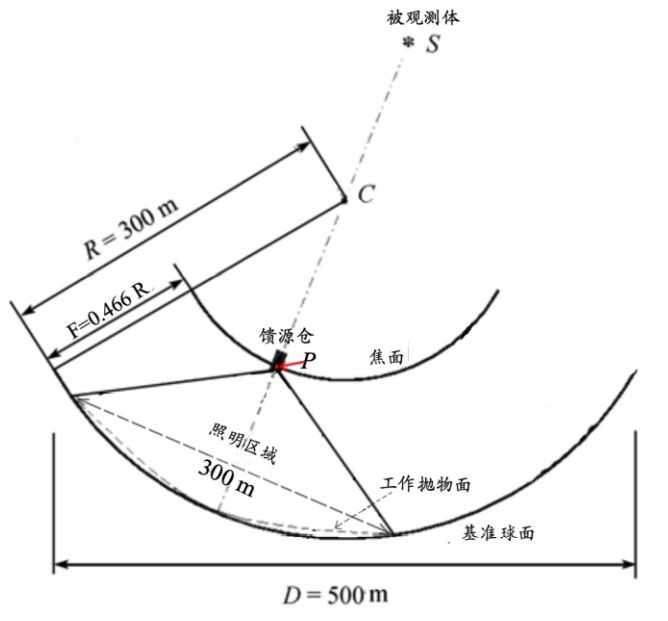
主动反射面可分为两个状态：基准态和工作态。基准态时反射面为半径约 300 米、口径为500 米的球面（基准球面）；工作态时反射面的形状被调节为一个 300 米口径的近似旋转抛物面（工作抛物面）。上图是 FAST 在观测时的剖面示意图，C 点是基准球面的球心，馈源舱接收平面的中心只能在与基准球面同心的一个球面（焦面）上移动，两同心球面的半径差为 F=0.466R（其中 R 为基准球面半径，称 F/R 为焦径比）。馈源舱接收信号的有效区域为直径 1 米的中心圆盘。当 FAST 观测某个方向的天体目标 S 时，馈源舱接收平面的中心被移动到直线 SC 与焦面的交点 P 处，调节基准球面上的部分反射面板形成以直线 SC 为对称轴、以 P 为焦点的近似旋转抛物面，从而将来自目标天体的平行电磁波反射汇聚到馈源舱的有效区域。

本赛题要解决的问题是：在反射面板调节约束下，确定一个理想抛物面，然后通过调节促动器的径向伸缩量，将反射面调节为工作抛物面，使得该工作抛物面尽量贴近理想抛物面，以获得天体电磁波经反射面反射后的最佳接收效果。

请你们团队根据附录中的要求及相关参数建立模型解决以下问题：
1、当待观测天体𝑆位于基准球面正上方，即𝛼 = 0°, 𝛽 = 90°时，结合考虑反射面板调节因素，确定理想抛物面。
2、当待观测天体𝑆位于𝛼 = 36.795°, 𝛽 = 78.169°时，确定理想抛物面。建立反射面板调节模型，调节相关促动器的伸缩量，使反射面尽量贴近该理想抛物面。将理想抛物面的顶点坐标，以及调节后反射面 300 米口径内的主索节点编号、位置坐标、各促动器的伸缩量等结果按照规定的格式（见附件 4）保存在“result.xlsx”文件中。
3、基于第 2 问的反射面调节方案，计算调节后馈源舱的接收比，即馈源舱有效区域接收到的反射信号与 300 米口径内反射面的反射信号之比，并与基准反射球面的接收比作比较。

数模国赛 思路和历程

为什么选A题？

虽然我是统计学专业的学生，但是对数据分析题不是非常感冒，而今年的B题看上去就是大家会偏爱的类型，连我在拿到题目之后，也花了几个小时分析其中的高维数据，但由于并没有很快的找到关键思路和方法，一想到会有很多人选B和C，最后还是坚定地选择了A题。至于为什么不选C，是因为对算法和离散优化问题不太了解，也不太会使用Mathematica进行离散优化的计算（其实就是很讨厌写算法就对了）。

对于A题，我最开始是如何考虑的

虽然在比赛前心中就有必选A题的信念，但看到题目内容之后，心里的确打了退堂鼓，原因有五：

1. FAST中反射面板、主索节点、促动器这些器件的机械关系是什么，是简单的线性关系吗？
2. 4000多块反射面板，如何解决如此大的计算量问题？
3. 0.07%的相邻节点变化幅度该如何考虑，是否可以大胆忽略？
4. 分析题目所给的数据，发现还有地形的坐标，是否需要考虑？如需要，该如何解决地形波动的影响？
5. Mathematica可以做这样的问题吗？如果不行，我应该用Matlab吗？

但由于第一问求理想抛物面的问题十分简单，只需联立两个方程即可算出，故可以先忽略以上的问题。

可以往下做的原因有三：

1. 第一问真的很简单，不会花费很久，有足够时间分析剩下的问题；
2. 通过分析附件的数据，主动反射面的坐标比较符合预期，方便计算；
3. 整体的思路已经有初步构思，基本上可以分为两个优化问题和一个几何计算问题。

总体的时间分配

这次采取了佛系建模的策略：

1. 第一晚确定选题和基本思路；
2. 后三天均为早10晚10.

第一问：理想抛物面的计算

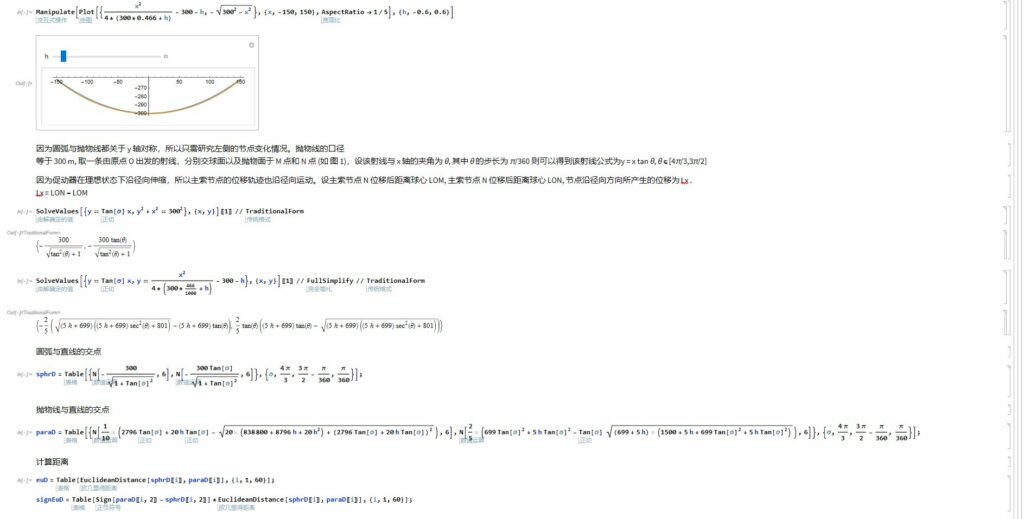
在第一问中，由于该问题是求理想抛物面的方程，我并没有使用附件中所给的数据进行计算,而是直接使用题中所给的理想模型进行分析。不难发现，球面和抛物面均是在$xoy$平面上各向同性的，那么可以将问题转化为二维进行分析，用圆弧代替基本球面、用抛物线代替抛物面。以基准球面球心作为坐标原点，圆弧和抛物面方程如下，球的半径为 R = 300m 且抛物面的口径也等于Dp = 300m, 如下图：

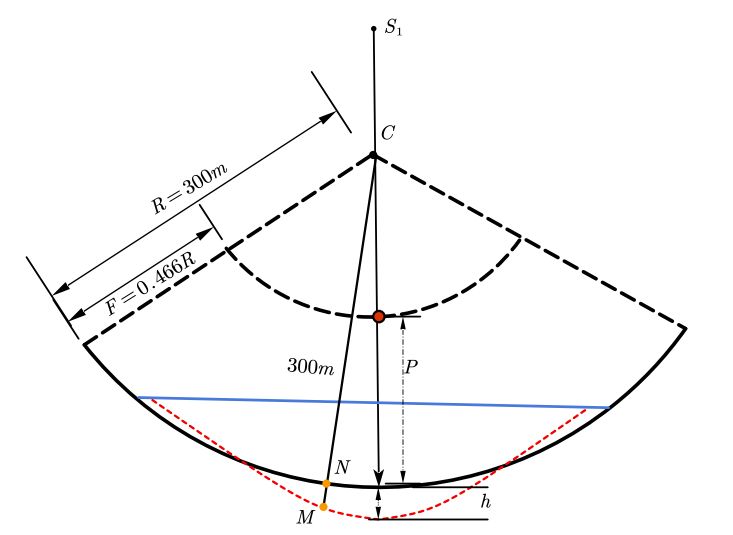
由于 F 与 R 已知，故该旋转抛物面的变化仅与抛物面顶点与基准球面的相对位置 h 决定。通过调整 h 的值，可以得到满足焦距条件的一簇旋转抛物面。这样我们就能将其转化为单变量优化问题。

下面是推导和计算的过程：

\left\{\begin{array}{l}
x^{2}+y^{2}=R^{2} \\
x^{2}+2 P y+2 P(R+h)=0
\end{array}\right.

其中 P 是馈源舱中点至基准球面底点的距离。可以解得：

y=\frac{x^{2}}{4(F+h)}-(R+h)

由于 F 与 R 已知，故该旋转抛物面的变化仅与抛物面顶点与基准球面的相对位置 h 决定。

主索点的位移模型

通过查阅论文，我们发现一般来说，主索节点的变形策略有如下几个：

1. 主索节点径向位移最小；
2. 抛物面弧长与切面弧长差最小；
3. 抛物面边缘与球面平滑过渡。

我们选择第一个，既从主索节点径向位移最小即促动器工作行程最短考虑，最开始建立了离散的优化，后面发现应该连续优化效果更好:

离散的处理方法

因为圆弧与抛物线都关于 y 轴对称，所以只需研究左侧的节点变化情况。抛物线的口径等于 300m, 取一条由原点 O 出发的射线，分别交球面以及抛物面于 M 点和 N 点 ，设该射线与 x 轴的夹角为 θ, 其中 θ 的步长为 $\frac{π}{360}$ 则可以得到该射线公式为:

通过调整$h$，这根射线与球面、抛物面的两个交点之间的距离最小是我们的优化目标。这一段不展开了，最后$h=0.38$左右。

连续的处理方法

由于求解这个离散问题的精度取决与 θ 的步长，而降低步长会显著增加计算复杂度，故将该问题等效转化为一个连续性问题，通过计算抛物面与球面间的面积，从而确定理想抛物面抛物面顶点与基准球面的相对位置 h（其实就是个积分求曲面面积的问题…）：

\underset{h}{\arg \min } \int_{-150}^{0}\left|-x \sqrt{R^{2}-x^{2}}-\frac{x^{2}}{4 *(F+h)}+R+h\right| d x

使用Mathematica计算，得到$h=0.39$.

那我们就能得到结果：

y=\frac{x^2}{560.762}-300.39

根据解析几何的知识，理想抛物面的方程为：

z=\frac{x^2+y^2}{560.762}-300.39

可以发现离散和连续计算的结果很相似。

问题二：选择节点、旋转变换和优化模型

选择节点

从题目中我们可以看到共有2226个主索节点，因为控制反射面是由主索节点进行的，所以只需要筛选出需要变换的节点，就可以减小计算量。

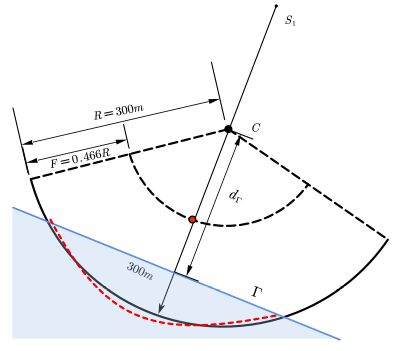
记切平面与基准球心 $C$ 的距离 $d_\Gamma$，设平面$\Gamma$表达式为：$Ax + By + Cz + D = 0$, 其中 $A = \cos α$, $B = \sin α$, $C = \tan β$.由题目所给信息可知，又因为基准球半径 $R = 300$, 基准球心作为坐标原点，根据勾股定理容易求得基准球心与平面$\Gamma$的距离. 关系式如下

D=d_{\Gamma}=\frac{\left|A x_{0}+B y_{0}+C z_{0}+D\right|}{\sqrt{A^{2}+B^{2}+C^{2}}}

在照明区域内的每一个主索节点的坐标 $(x_i, y_i,z_i)$ 都满足以下条件：

A x_{i}+B y_{i}+C z_{i}+D \leqslant 0 \\ 代入得\quad 0.800784 x+0.598954 y+4.77383 z+1267.2 \leqslant 0

经过计算，我们最终得到了699个节点。

旋转矩阵，我为什么需要它？

还记得在第一问中的抛物面方程吗？它的顶点在z轴。如果，如果让你写出一个如上图红色虚线所示的抛物线方程，你会咩？（反正我不会）

所以我就想着用三维的坐标变换，把所有节点全部变换到以z轴为顶点的抛物面上（与第一问相似），这样我们就可以沿用第一问的抛物面方程继续进行单目标优化了（对，居然和第一问一样哈哈哈xswl）基于这样的考虑，我才有着继续做下去的勇气（暴风哭泣）。

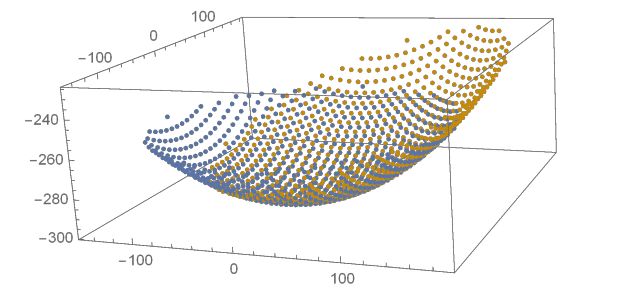
至于怎么变换咩，看看下面吧！

绕 $z$ 轴进行逆时针旋转 $θ_1$ 角度时，记 $R_z(θ_1)$ 为旋转矩阵，则满足下列等式：

\begin{array}{l}
R_{z}\left(\theta_{1}\right)=\left[\begin{array}{ccc}
\cos \theta_{1} & -\sin \theta_{1} & 0 \\
\sin \theta_{1} & \cos \theta_{1} & 0 \\
0 & 0 & 1
\end{array}\right] \\
z^{\prime}=R_{z}\left(\theta_{1}\right) z
\end{array}

绕 $y$ 轴进行逆时针旋转 $θ_2$ 角度时，记 $R_y(θ_2)$ 为旋转矩阵，则满足下列等式：

\begin{array}{l}
R_{y}\left(\theta_{2}\right)=\left[\begin{array}{ccc}
\cos \theta_{2} & 0 & \sin \theta_{2} \\
0 & 1 & 0 \\
-\sin \theta_{2} & 0 & \cos \theta_{2}
\end{array}\right] \\
y^{\prime}=R_{y}\left(\theta_{2}\right) y
\end{array}

绕$ x$ 轴进行逆时针旋转 $θ_3$ 角度时，记 $R_x(θ_3)$ 为旋转矩阵，则满足下列等式：

\begin{array}{l}
R_{x}\left(\theta_{3}\right)=\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \theta_{3} & -\sin \theta_{3} \\
0 & \sin \theta_{3} & \cos \theta_{3}
\end{array}\right] \\
x^{\prime}=R_{x}\left(\theta_{3}\right) x
\end{array}

三维旋转矩阵可通过公式 (23) (24) (25) 相乘得到，于是在旋转后的新坐标可表示为：

\begin{array}{c}
{\left[\begin{array}{c}
x_{n} \\
y_{n} \\
z_{n}
\end{array}\right]=W\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]} \\
W=R_{x}\left(\theta_{3}\right) R_{y}\left(\theta_{2}\right) R_{z}\left(\theta_{1}\right)
\end{array}

其中的$W$就是通过代入角度求三个矩阵相乘得到的结果，用Mathematica大概是这样做的：

RotationMatrix[{{0, 0, 1}, {Cos[36.795 \[Degree]], 
Sin[36.795 \[Degree]], Tan[78.169 \[Degree]]}}] // MatrixForm

有了变换后类似第一问的模型，还是不能完全按照第一问的方法去做，这是因为现在每个节点是离散分布在面上的，所以需要对每一个主索节点进行优化考虑。

主索节点坐标的优化

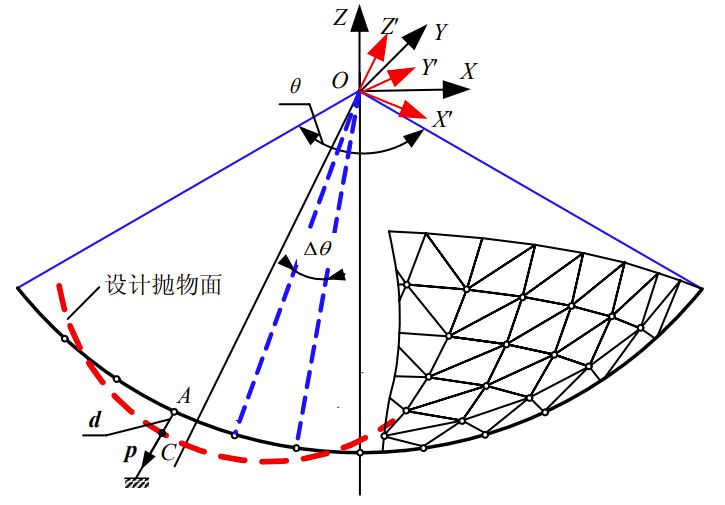
可以从图中看到，对于任意主索节点$A$, $-\mathbf{p}$指向球心，调整时改变的偏差量$d$，按照$\mathbf{p}$的方向径向进行。如果将基准态时的坐标$A$记作$(x,y,z)$，调整后的坐标记作$N(x_0,y_0,z_0)$，我们可以得到如下方程组：

\left\{\begin{array}{l}
x_{0}=x+p_{x} d \\
y_{0}=y+p_{y} d \\
z_{0}=z+p_{z} d
\end{array}\right.  \rightarrow A=N+\mathbf{p}d

由于工作态反射面为旋转抛物面，所以$A$点经过调整后的到的$N$点位于工作抛物面上，于是 $N$满足理想抛物面方程, 从而解得偏差量 $d$的表达式：

z+p_{z} d=-\frac{\left(x+p_{x}\right)^{2}+\left(y+p_{y}\right)^{2}}{4(F+h)}-300-h

为了使得工作状态的主索网能够最接近理想抛物面，设置优化的目标函数为主索节点表面与理想抛物面的均方根误差最小(查阅文献)，均方根误差计算式如下:

\delta_{c}=\sqrt{\Delta_{c}^{\mathrm{T}} \Delta_{c} / n}

其中，$n$表示在照明区域内的总节点个数，$\Delta_c$是照明区域内节点的偏差分布向量, 满足

\boldsymbol{\Delta}_{c}=\left[\boldsymbol{d}_{c 1}^{\mathrm{T}}, \boldsymbol{d}_{c 2}^{\mathrm{T}}, \cdots, \boldsymbol{d}_{c n}^{\mathrm{T}}\right]^{\mathrm{T}}

综上可知，目标优化函数为

\underset{h}{\arg \min } \delta_{c}(h)=\sqrt{\Delta_{c}^{\mathrm{T}} \Delta_{c} / n}

解这样一个单目标优化问题，会发现均方误差最小的时候h已经超出了最大上限，所以取最大上限0.6m.

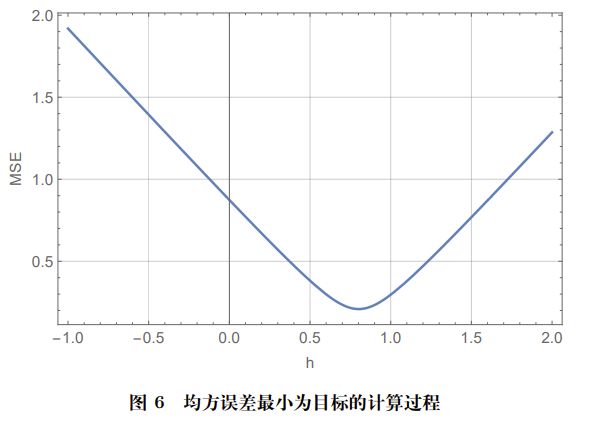
算出h之后，每一个变换后坐标就能够直接求出了，这时候，我们右乘旋转矩阵作逆变换，就可以得到结果啦！这也是使用旋转矩阵的一个原因——逆变换很方便。

这样我们得到到理想抛物线顶点坐标为：(−49.32, −36.8894, −294.018)。

第三问：平面反射模型

这一问实在是让人捉摸不透，信号比到底是个什么东西歧视问题里没有说的很清楚，所以我就算了两种。

1. 每个被馈源舱接受的平面反射信号占总反射信号的比：对于每一个反射面反射出的信号，计算投影至馈源舱圆盘上的面积并求和，再计算每一块反射面投影至馈源舱圆盘平面上的面积并求和，将这两个面积作比，记为接收比。
2. 每个平面反射信号占馈源圆盘的比：对于一个反射面反射出的信号，计算投影值至馈源舱圆盘的面积，并域馈源盘面面积相比，求和后作平均，记为接收比。

简单来说，就是一个是考虑所有反射信号，计算打到圆盘上的信号的百分比，这个百分比可能会很小因为圆盘很小。第二个信号比是只考虑达到圆盘上的信号，这些信号占整个圆盘的面积的均值，这个百分比会相对大很多，如果所有信号覆盖了圆盘，那百分比就为100%。

倒是用了Blender模拟了一下信号在馈源舱处的图像（RTX ON!)

考虑到每块反射平面是由三个主索节点构成的三角形，而信号视为直线传播，沿垂直方向射向反射面，可以在此条件下构建信号反射模型。

对任一由 $P_1 = (x_1, y_1, z_1), P_2 = (x_2, y_2, z_2), P_3 = (x_3, y_3, z_3)$ 构成的平面 $\Gamma$, 分别计算两点构成的向量，

\begin{array}{c}
\mathbf{n 1}=\left(x_{2}-x_{1}, y_{2}-y_{1}, z_{2}-z_{1}\right) \\
\mathbf{n 2}=\left(x_{3}-x_{1}, y_{3}-y_{1}, z_{3}-z_{1}\right) \\
{[a \quad b\quad c]^{\mathrm{T}}=n_{1} \times n_{2}}
\end{array}

并对两个向量进行叉积和标准化, 得到该平面的单位法向量:

\mathbf{n}_{\Gamma}=\frac{a b}{\sqrt{\sum\left(a^{2}+b^{2}\right)}}

对于\Gamma平面中的 $P_1$ 点，入射信号的单位向量为 $\mathbf{v}_{in} = (0, 0, −1)$, 而出射信号的方向沿穿过 $P_1$ 点的单位法向量对称，如上图。

由于馈源舱在 $z$ 轴上的坐标可以通过 $F − R$ 求得，根据反射定理中入射角等于出射角以及馈源舱所在平面的位置关系等，可以计算出出射信号的单位向量为：

\mathbf{v}_{out}=(2ac,2bc,1-2(a^2+b^2))

根据单位向量与实际坐标的数量关系，可以得到

\left\{\begin{array}{l}
\frac{2 a c}{Q_{x}-x_{1}}=\frac{1-2\left(a^{2}+b^{2}\right)}{Q_{z}-z_{1}} \\
\frac{2 b c}{Q_{y}-y_{1}}=\frac{1-2\left(a^{2}+b^{2}\right)}{Q_{z}-z_{1}}
\end{array}\right.

其中 $Q_z = F − R$.

根据上述方程组，我们可以得到 $Q_x, Q_y$ 的坐标分别为：

\begin{aligned}
Q_{x} &=\frac{2 a^{2} x_{1}+2 b^{2} x_{1}+2 a c z_{1}+2 a c Q_{z}-x_{1}}{2 a^{2}+2 b^{2}-1} \\
Q_{y} &=\frac{2 a^{2} y_{1}+2 b^{2} y_{1}+2 b c z_{1}+2 b c Q_{z}-y_{1}}{2 a^{2}+2 b^{2}-1}
\end{aligned}

这样我们就得到了平面一个端点射到馈源舱平面的信号的xy坐标。计算三个就可以表示整个平面的反射啦（仿射变换的知识）。后面计算信号比是很无聊的工作，多亏了Mathematica中的图形处理功能，可以把很多个三角形作交并集，计算量减少很多，而且可以直接离散化求面积，真是让我猛男落泪。

当然，有第二问旋转矩阵那么好的工具，在第三问里我们也用到了，下面是几张图。

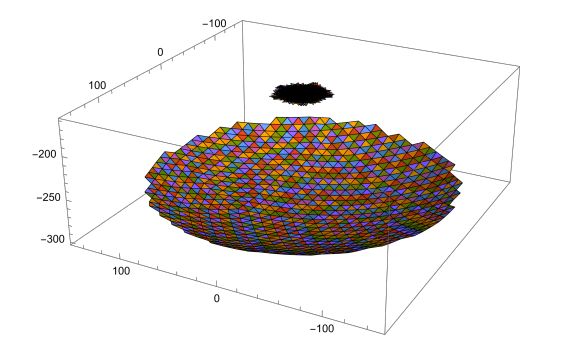
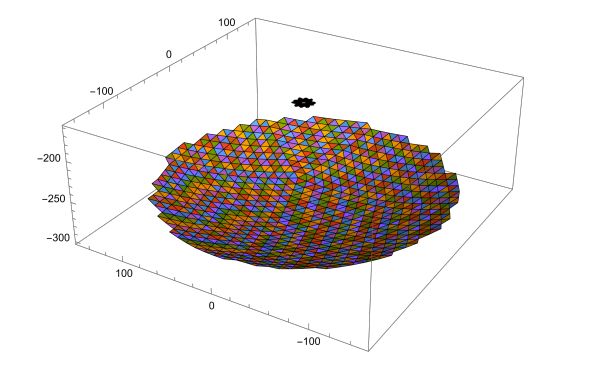
关于第三问的一些后话

比赛结束之后，网上有讨论的声音，A题最大的问题就是第三问反射面到底是平面还是曲面，我阅读问题的时候，并没有发现有任何暗示或是明示要将其考虑成曲面，但是算出来只有1.1%的结果的时候，其实还是有点慌的，所以自作主张的加入了第二种信号比的计算方法，答辩的时候还被特意问到，好险我讲清楚了… 不然是要触雷的QAQ

总结

说实话今年的A题很适合使用Mathematica来做，推公式、算反射、加矩阵变换都很简单，而且结果准确度相当高！

至于之前的五个问题，我现在来回答一下：

• FAST中反射面板、主索节点、促动器这些器件的机械关系是什么，是简单的线性关系吗？

是的，需要考虑的仅仅是h和对应的d而已。

• 4000多块反射面板，如何解决如此大的计算量问题？

其实考虑的是主索节点，2000多个，但是第二问第三问经过筛选，只需要考虑700个左右。

• 0.07%的相邻节点变化幅度该如何考虑，是否可以大胆忽略？

可以，本来就是分米级的变动，0.07%不得到微米级？我的结果已经精确到毫米级了，是时候满足了~（大霧，其實問題還是挺複雜的

• 分析题目所给的数据，发现还有地形的坐标，是否需要考虑？如需要，该如何解决地形波动的影响？

不用，只是用来吓人的…

• Mathematica可以做这样的问题吗？如果不行，我应该用Matlab吗？

完全！可以！看了看优秀论文用的Matlab，感觉很麻烦捏~

下面是一些有趣的图，截取自MMA代码~

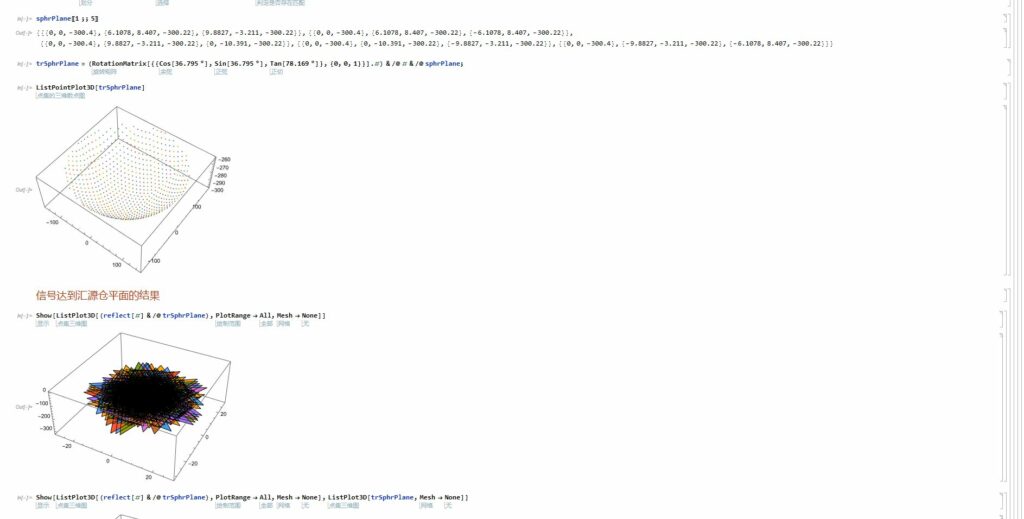
什么？你看到这了？说不定你想要Mathematica代码，下面下载哦~

更新：其實這個反射面的問題，并沒有當時比賽的時候想的那麽簡單，希望能夠抛磚引玉，期待更好的解決方法。

最后的最后，2021年几道题的评审要求和细节：https://blog.csdn.net/youcans/article/details/120185296