从一个方程说起
考虑如下方程的在复数域解:
1=z^{3}我们有:
z=1,z=(-1)^{2/3},z=-(-1)^{2/3}乍一看来, 只有第一个解是可以立马得到的, 而剩下的两个解则需要一些运算。
如果遇到z_0=z^{n}这样的方程, 他有什么特质呢?
复数域上的变换
回到第一个方程, 我们可以看到对z做变换f:x\rightarrow x^3, 这对于复数代表了什么含义?
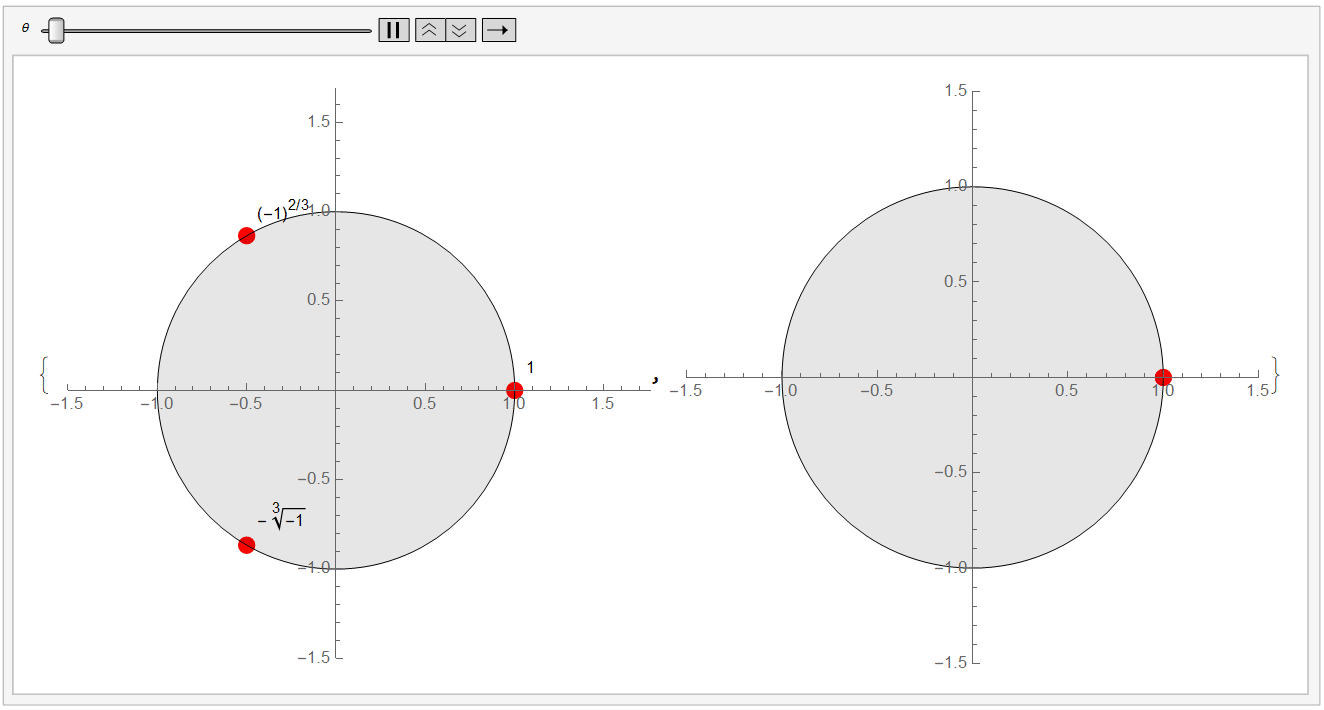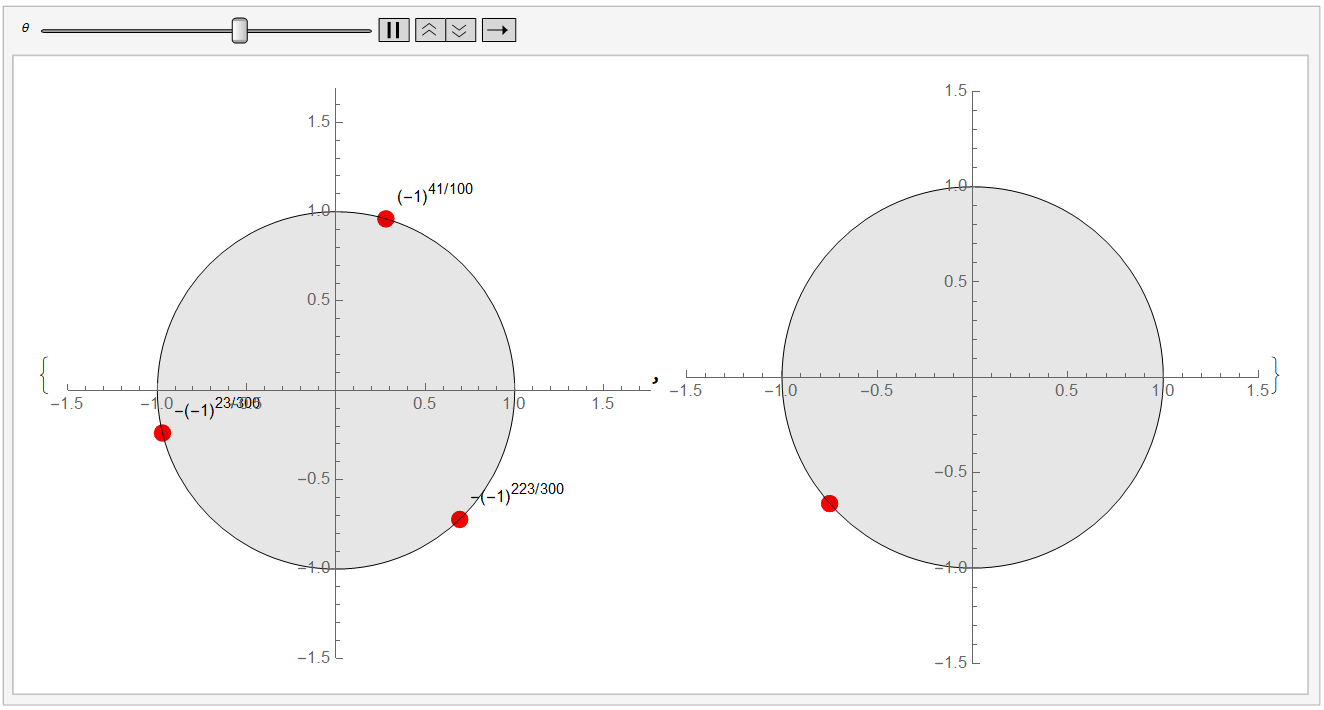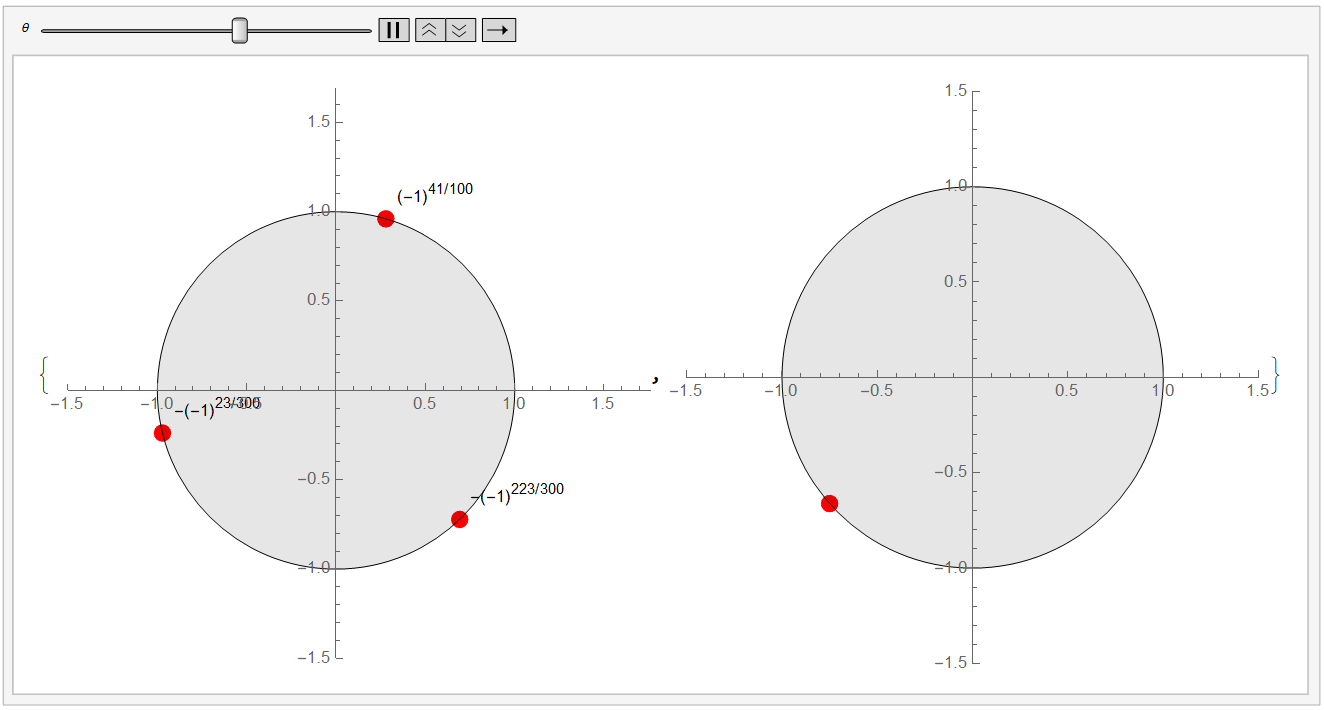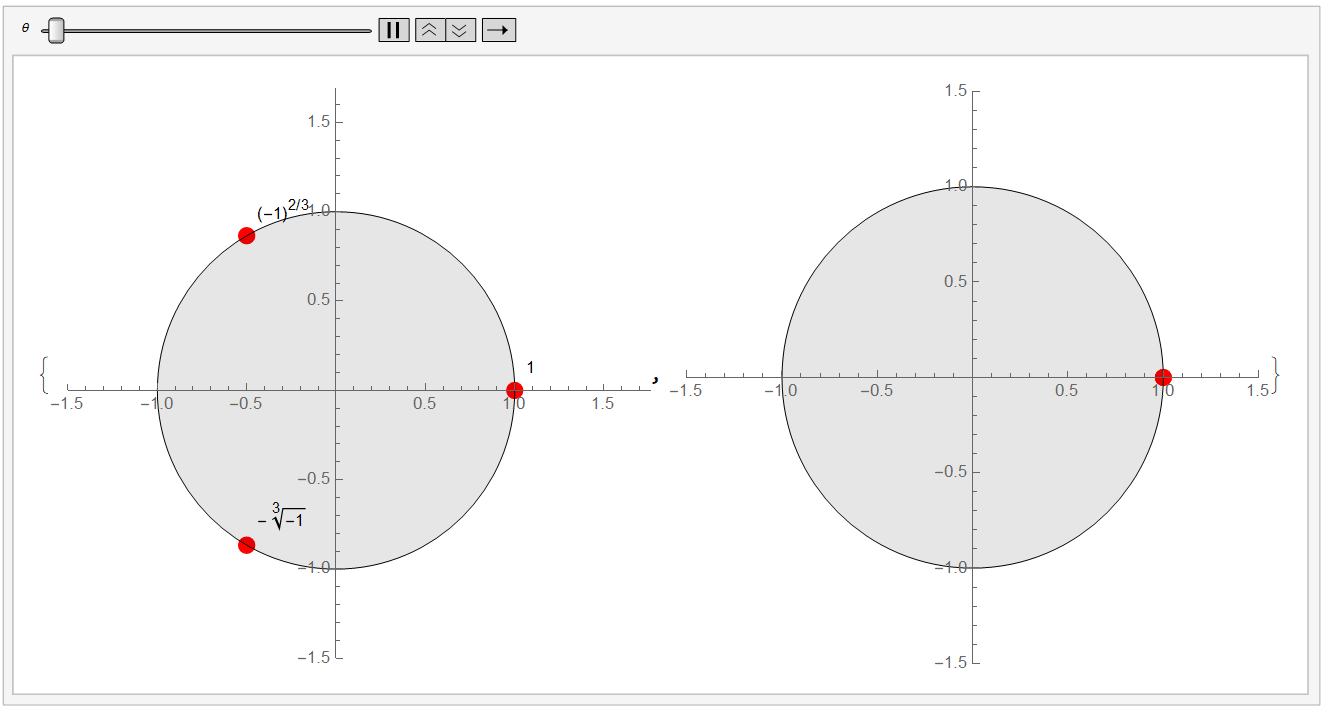
让我们将方程的三个解绘制出来, 再加上单位圆,我们得到了如下图像:
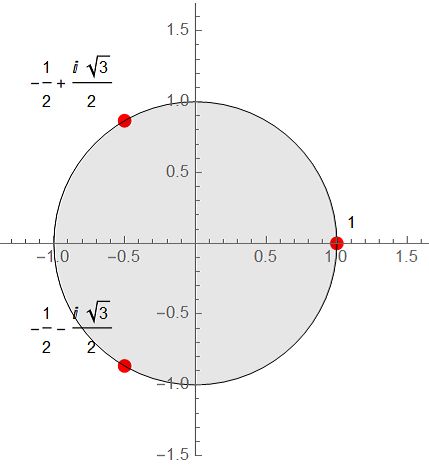
明显的,这三个点在圆上构成了一个正三角形。
如果令w=f(z)=z^n,则z^(n)=1的解正是z平面上被映到w平面上的w=1的那些点。
对于更多情况的讨论
直接放两张动图你就懂了。