重新发明复数 篇六 复数域上的收敛性上篇

从一些例子引入收敛半径

I. 例子A

考虑一个多项式函数f(x)=\frac{1}{x-1}, 它的泰勒级数为\textbf{Series}(f)=1+x^2+x^3+···

再考虑一个三角函数g(x)=\cos(x)的泰勒级数\textbf{Series}(g)=1+\frac{x^2}{2!}+\frac{x^4}{4!}+···

要知道级数利用了函数在x=x_0处的任意阶导数信息，所以我们可以猜测拥有了任意阶导数信息之后，由无穷项多项式是不是可以无限接近原函数呢?

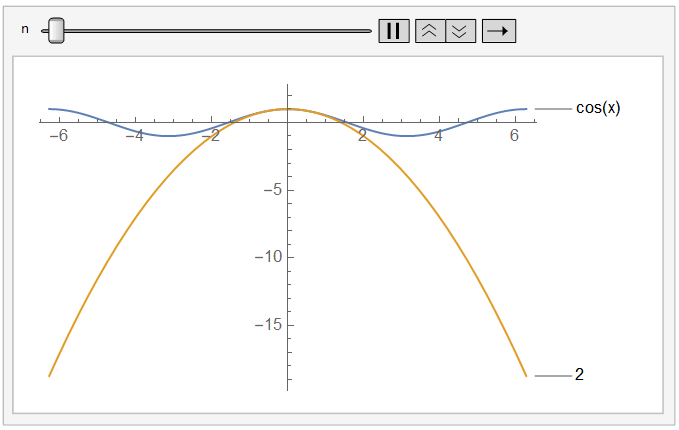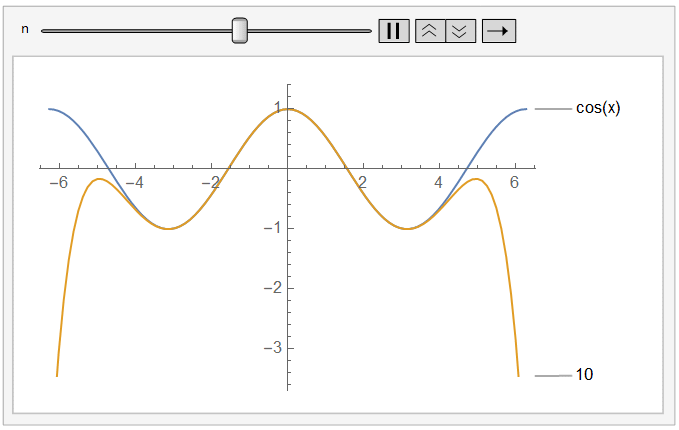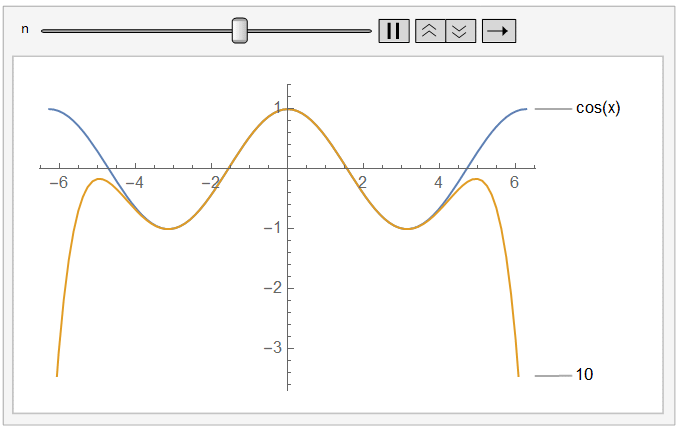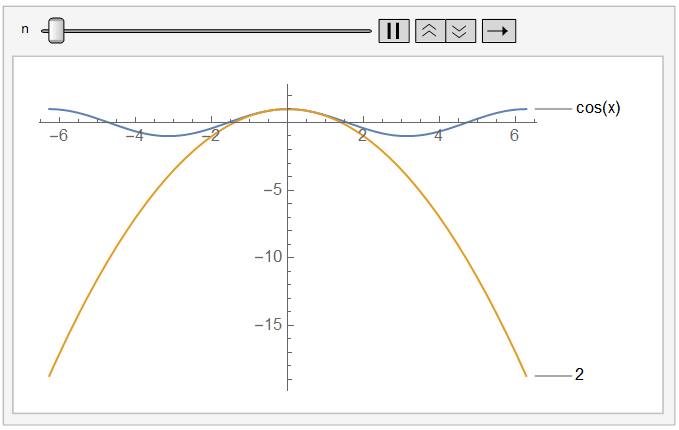
对于g(x)来说, 似乎是这样的,随着多项式阶数的不断增加，相似的区间不断增加，我们有理由相信其随着阶数的增加，还会不断扩张。

[gif-player id=”1008″]

看起来我们的猜测是正确的，那么f(x)呢?

[gif-player id=”1010″]

随着多项式阶数的增大，在(-1,1)这个区间里，的确更接近了，但在这个区间之外，增加的项数并没有办法更好的拟合其他区域。在这里，我们知道多项式函数一定是一个连续函数，不会存在间断点，而对于有间断点的不连续函数，当项数为无穷(虽然这没什么意义)时，也没办法模拟出有间断点的情况。

看来对于某些函数(目前看来尤其是在\mathbb{R}上不连续的函数)，级数是无法对整个函数进行拟合的。而我们定义收敛域为\sum^{\infty}_{n=1}{u_n(x)}的所有收敛点的集合。

等等，为什么我听到的总是收敛半径?

虽然在某些情况下，收敛半径不是收敛域的一半，但是在大多数情况下，收敛半径是收敛域的一半。

这话说的很危险，之后会详细叙述。

II. 例子B

我们在之前讨论过，不连续的函数应该有收敛域，那么对于连续函数，收敛域一定是\mathbb{R}吗?

考虑两个函数f(x)=\frac{1}{1-x^2}，g(x)=\frac{1}{1+x^2}

它们的级数为\textbf{Series}(f(x))=1+x^2+x^4+···，\textbf{Series}(g(x))=1-x^2+x^4-···

很显然可以知道这个f(x)=\frac{1}{1-x^2}的收敛域为(-1,1) 收敛半径为1.

很反常的，我们能够发现这个连续函数的收敛域也是(-1,1)且收敛半径为1，这与上面的结果是相同的。

但是这个函数是连续的，按理说应该能够被某一多项式函数完全描述，观察(1+x)^2的解，我们又找到了一条通向复数域的道路。

A way lead to Complex Region

首先按x=k展开为幂级数，把结果写成\sum^{\infty}_{j=0}{c_jX^j},其中X=(x-k)是k到x的距离。

为了展开g(x), 我们先在k处展开\frac{1}{a-x}:

\frac{1}{a-x}=\frac{1}{a-(X+k)}=\frac{1}{a-k}\frac{1}{[1-\frac{X}{a-k}]} \\
=\sum^{\infty}_{j=0}{\frac{X^j}{(a-k)^{j+1}}} \\
\textbf{where}\space |X|<|a-k|

那么我们的g(x)有:

\frac{1}{1/x^2}=\frac{1}{2}[\frac{1}{1-x}-\frac{1}{-1-x}]\\
=\frac{1}{2}\sum^{\infty}_{j=0}{[\frac{1}{(1-k)^{j+1}}-\frac{1}{(-1-k)^{j+1}}]X^j}\\
\textbf{where}\space |X|<|1-k|\space \textbf{and} \space |X|>|1+k|

所以收敛半径为R=\min (|1-k|,|1+k|)

这张图很好的展示了k和R的关系:

[gif-player id=”1021″]

至于g(x)的收敛半径，我们不加证明的给出其结果:R=\sqrt{1+k^2}. 我们见过它，他就是复平面上点(k,0)到(0,i)的距离!

那么我们可以得到

[gif-player id=”1023″]

至于为什么会这样, 看看g(x)在复数域上的图像就能明白.

虽然在实数域上(黑色直线)没有遇到奇点, 但是在复数域上该方程是有奇点的，这就说明了为什么上面讨论的函数有收敛区间并且半径为1。

我们看到的只是宏伟建筑中的一堵墙，推倒它才能看到全景。

下篇我们会更严格的讨论收敛圆的问题，并以更严肃的推导来描述这些名词:

绝对收敛, 一致收敛···

Reference

Visual Complex Analysis