从收敛区间到收敛圆
神敲开实数的墙,创造了无上的圆。
我们在上一篇文章中讨论了f(x)=\frac{1}{x^2-1}的收敛性,我们可以看到,对于|f(x)|来说(一般来说,加绝对值不会对收敛区间有改变),其收敛区间与爆破点的紧密联系:
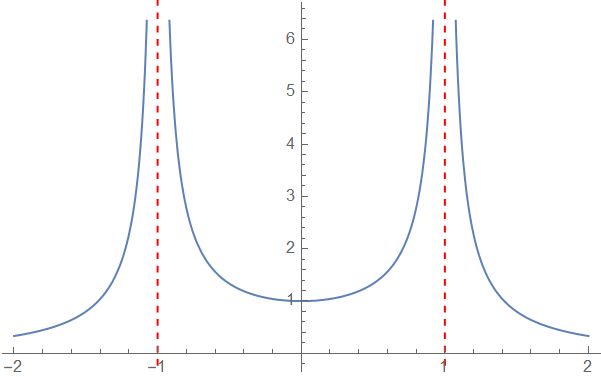
让我们在复数域上看看收敛区间是如何拓展的.
让我们直接对f(x)展开,使用最高项为10次来绘制图像, 可以得到下面的图像:
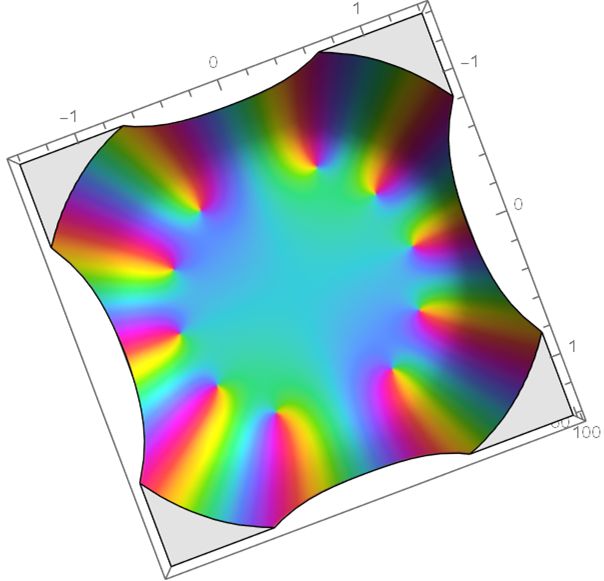
我们来对这张图进行详细的分析, 首先我们定义逆时针彩虹色为零点(\displaystyle \lim_{x=a}{f(x)=0}), 可以看到该图中共有10个零点,这与我们最高项为10次相对应。而这十个点隐喻地构造了一个圆。
显然的,这与我们的收敛圆有相当大的关系。让我们严肃地探讨它们的联系。
一些定义
对于给定的值z=a, 如果对任意给定的正数\epsilon, 不论其多么小, 总存在一个正整数N, 使对每个大于N的值n恒有|A-P_n(a)|<\epsilon, 我们就说点P_1(a),P_2(a),P_3(a),···的序列收敛于点A. 反之,我们说其发散.
What?
考虑这样一个点列和收敛圆,如果对点列标号(这里越靠近原点的点标号越大),我们发现进入圆后(大于一个特定的标号N),点列收敛到了一点A.
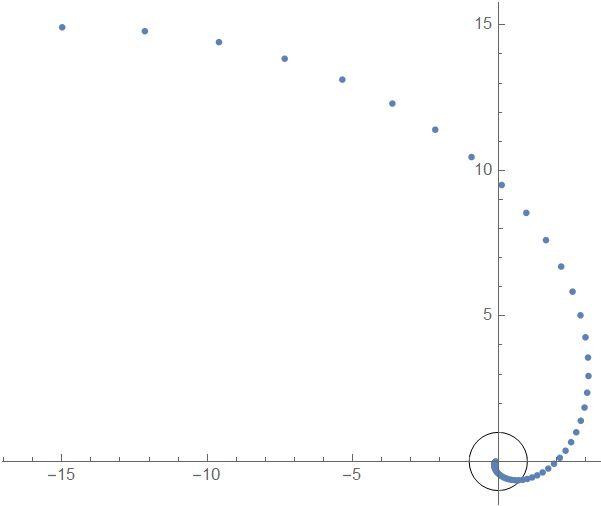
绝对收敛
幂级数P(a)在z=a处绝对收敛, 如果实级数
\displaystyle P(z)=\sum^{\infty}_{j=0}{|c_jz^j|}=|c_0|+|c_1z|+|c_2z^2|+|c_3z^3|+···在该处收敛.
且
若P(z)在某点绝对收敛, 则它在该点必收敛.
这是由于|P_n(a)-Pm(a)|\leq |c_{m+1}a^{m+1}|+···||c_na^n|
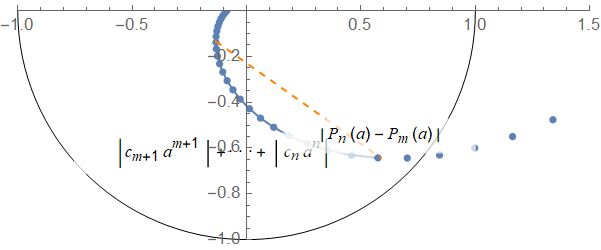
那么我们可以说
若P(z)在z=a处收敛, 则它在圆盘|z|<|a|内处处收敛. (在圆周|z|=R上的敛散性无法由此确定)
将此结果推广到任一点k为中心的幂级数, 我们有
已给以k为中心的复幂函数P(z), 必存在一以k为中心的圆周|z-k|=R, 使P(z)在其内域处处收敛, 而在外域处处发散.
最后, 在讨厌的定理说明结束之前, 再不加证明地抛出一个关于一致收敛的结论
若P(z)收收敛圆盘|z|<R, 则P(z)在任意小的圆盘|z|≤r中恒一致收敛, 这里r<R.
这样, 我们就将原本在实数域上的幂级数收敛性拓展到了复数域上.
如何求收敛半径?
计算方法
在实数域上讨论收敛半径是奇怪的, 因为没有圆, 哪来的半径?
但我们还是有一些方法来求收敛半径.
比式判别
\displaystyle R=\lim_{n\rightarrow \infty}|\frac{c_n}{c_{n+1}}|根式判别
\displaystyle R=\lim_{n\rightarrow \infty}\frac{1}{\sqrt[n]{|c_n|}}柯西-阿达玛判别
\displaystyle R=\frac{1}{\lim \sup \sqrt[n]{|c_n|}}但根据我们的经验, 可以得到一个更明显的事实.
实用方法
若f(z)可以表示为一个中心在k的幂级数, 则收敛半径是从k到f(z)最近奇点的距离.
借此我们终于可以推导出f(x)=\frac{1}{1+z^2}这样一个在实数域上连续的函数是如何有收敛半径为1的中心为0的幂函数, 又是如何在复数域上进行推演和收敛圆的表示的. 我们还可以解决在之前提到的, 对以k为中心的幂函数, 收敛半径为R=\sqrt{1+k^2}.
我们仍对f(x)=\frac{1}{1+x^2}进行讨论.(对于实数域我们使用x,复数域则使用z)
我们沿用在实数域上的方法, 可以得到
\displaystyle \frac{1}{a-z}=\sum^{\infty}_{j=0}{\frac{Z^j}{(a-k)^{j+1}}} \\
\textbf{iff} \space |Z|<|a+k|将\displaystyle \frac{1}{1+z^2}展开我们有
\displaystyle \frac{1}{1+z^2}=\frac{1}{(z-i)(z+i)}=\frac{1}{2i}[\frac{1}{-i-z}-\frac{1}{i-z}]这样我们就可以按照上面的模式得到
\displaystyle \frac{1}{1+z^2}=\sum^{\infty}_{j=0}{\frac{1}{2i}[\frac{1}{-i-k^{j+1}}-\frac{1}{(i-k)^{j+1}}]Z^j}f(z)收敛当且仅当两个展开的幂级数相等, 那我们有
R>|z-k|. 这里的R就是幂级数中心k到最近奇点的距离.
当k是实数时, 我们就有|i-k|=\sqrt{1+k^2}.
最后, 从图中我们检查该结论是否正确.

可以看出, 如果中心在实数上移动, 这些圆的轨迹都通过\pm i, 即f(z)的奇点.
References
Visual Complex Analysis
Wolfram Research (2019),ComplexPlot3D,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ComplexPlot3D.html (更新于 2020 年).
