为什么是参数方程?

前言

复习解析几何时，有件事情总想不明白——为什么有了各种方程之后，还要加上一种麻烦的、拥有辅助变量的参数方程。
比如说，这个球面方程

x^2+y^2+z^2=1

再经过参数化之后就会变为

\left\{\begin{matrix}
 x=r\cos\phi\cos\theta \\ y=r\cos\phi\sin\theta \\ z=r\sin\phi
\end{matrix}\right.
\\(\phi,\theta) \in [-\frac{\pi}{2},\frac{\pi}{2}]\times[-\pi,\pi) 

看起来复杂了很多，而且好像没什么意义…

对于一般的二维直线方程, 或是三维直线方程, 看起来倒是挺直观, 可是这个t到底代表了什么呢?

非线性变换

没错，而且是对坐标轴的非线性变换~
我们来举个例子:
对于一个抛物线，我们有y^2=x
它的参数方程为:

\left\{\begin{matrix}
x=t^2\\
y=t
\end{matrix}
\right.

这意味什么?
考虑到y=t, 它的图像为

然后考虑x=t^2,

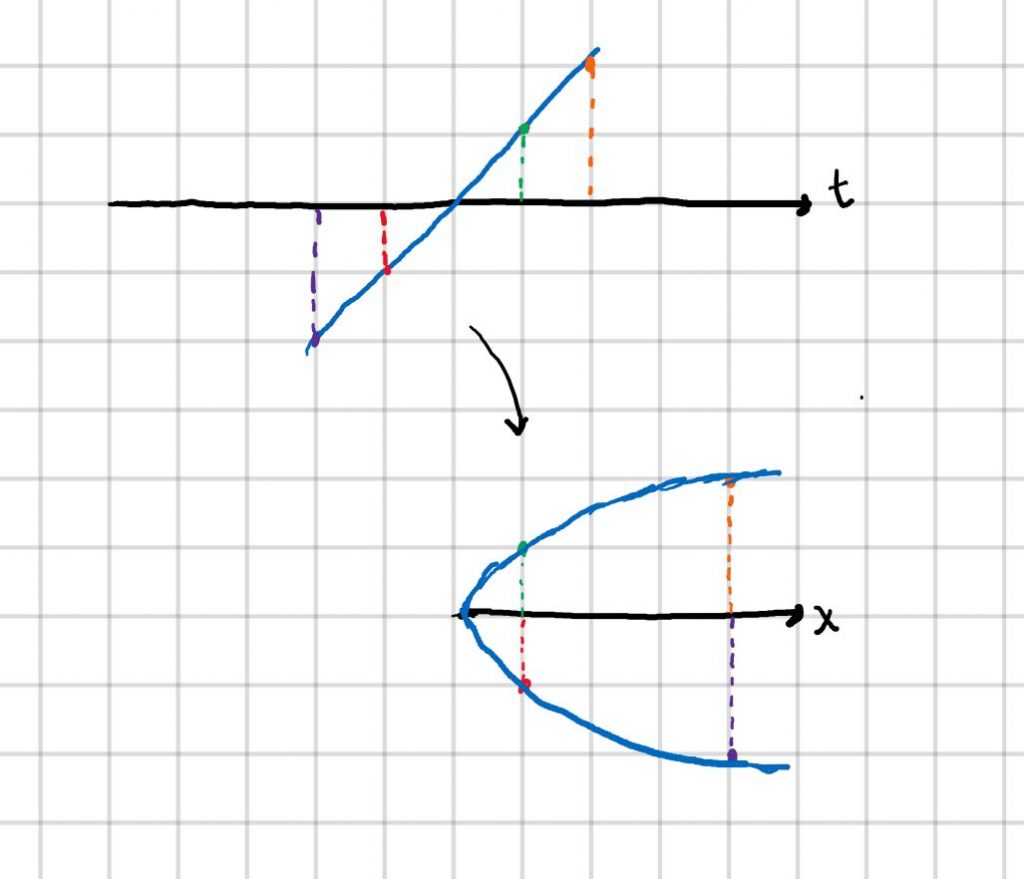
这样看起来, 就相当于使用了一个中间变量, 将原本不满足“单射”的隐函数函数转化成了几个满足"单射"的显函数的集合。