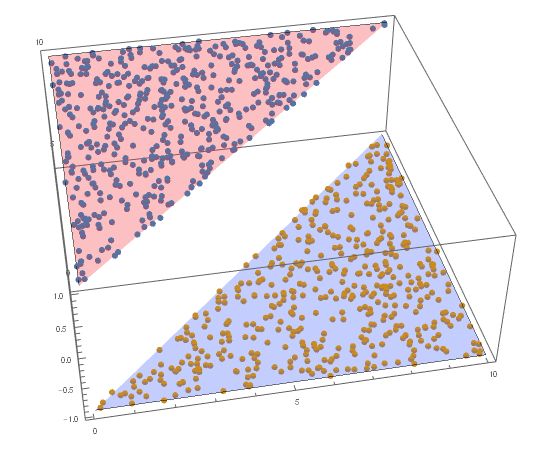
What is a preceptron?
Suppose we have a linearly separable two-category dataset with an input space \mathcal{X}\subseteq\mathbb{R}^n and a output space \mathcal{Y}=\{+1,-1\}, preceptron tries to find a hyper-plane that can completely seperate these two class (-1 and 1). Here is a intutive plot of it:

The hyper-plane cuts the dataset into two parts with the values of -1 and 1, that white vacancy is the imagined hyper-plane.
The Model
As we give the input and the output space above, the function for that reflection is:
f(x)=\mathrm{sign}(w\cdot x+b)Here the \cdot stand for inner product of two vector, w for weight vector and b for bias.
Plus, the \mathrm{sign} here is the sign function:
\begin{cases}
& +1,x\ge 0 \\
& -1,x< 0
\end{cases}For a given dataset T where T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}, preceptron model is to get the w,b that satisfy the classfication requires. Then using the model to forecast any given data is avaliable.
The Strategy
Linear Separability
For a given dataset
T=\{(x_1,y_1),...(x_N,y_N)\}If it exists a hyper-plane that can completely divide dataset into positive and negative subsets, in which for all
i\space\text{that}\space y_i=+1\space\text{s.t.}\space w\cdot x_i+b>0, we consider this a linearly separable data set, and vice versa.
The Loss Function
Distance
For a random point x_0 in the input space \mathbb{R}^n, we have the distance to the given hyper-plane S is
\frac{1}{||w||}|w\cdot x_0+b|For misclassified data, -y_i(w\cdot x_i+b)>0, so the distance to the hyper-plane is
\frac{1}{||w||}y_i(w\cdot x_i+b)Let M be the set contains all the misclassified data, the total distance would be
\displaystyle -\frac{1}{||w||}\sum_{x_i\in M}y_i(w\cdot x_i+b)Dismiss \frac{1}{||w||}, we have the loss function
\displaystyle L(w,b)=-\sum_{x_i\in M}y_i(w\cdot x_i+b)The Algoritm
The algoritm of preceptron is a optimization-algoritm, which is, calculating the parameters w,b by minimizing the loss function
\displaystyle \min_{w,b}L(w,b)=-\sum_{x_i\in M}y_i(w\cdot x_i+b)Here we use stochastic gradient descent to find the minimum of the loss function
\displaystyle \nabla_wL(w,b)=-\sum_{x_i\in M}y_ix_i\\
\nabla_wL(w,b)=-\sum_{x_i\in M}y_iIn this case the update of w and b would be
w\leftarrow w+\eta y_ix_i\\
b\leftarrow b+\eta y_iWhere \eta(0<\eta\leq1) is the stepsize (some would like to say learning rate).
The Dual Problem
In the primary problem, when the procedure stops, the final w,b will be
\displaystyle w=\sum^{N}_{i=1}\alpha_i y_i x_i\\
\displaystyle b= \sum^{N}_{i=1}\alpha_i y_iSo we can conclude a model like
\displaystyle f(x)=\mathrm{sign}(\sum_{j=1}^N \alpha_iy_jx_j\cdot x+b)\\
\mathrm{where}\quad \alpha = (\alpha_1,\alpha_2,...,\alpha_N)^TAnd the condition would be like
\displaystyle y_i(\sum^N_{j=1}\alpha_jy_jx_j\cdot x_i+b)\leq 0We only need the inner product of each data, and store them in a matrix call the Gram.
G=[x_i\cdot x_j]_{N\times N}