树的概念
什么是树?
树属于非线性数据结构的一种,概念也极多,是由结点或顶点和边组成的且不存在着任何环的一种数据结构。
没有结点的树称为空树。一棵非空的树包括一个根结点,还很可能有多个附加结点,并且所有结点构成一个多级分层结构。
树的定义
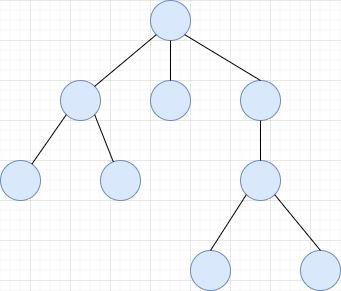
n个节点组成的有限集合。n=0,空树;n>0,1个根节点,m个互不相交的有限集,每个子集为根的子树,如图所示为一颗树:

树的基本术语
- 节点的度: 树中某个节点的子树的个数;
- 树的度: 树中各节点的度的最大值;
- 分支节点: 度不为零的节点;
- 叶子节点: 度为零的节点;
- 路径: i->j;
- 路径长度: 路径经过节点数目减1;
- 孩子节点: 某节点的后继节点;
- 双亲节点: 该节点为其孩子节点的双亲节点(父母节点);
- 兄弟节点: 同一双亲的孩子节点;
- 子孙节点: 某节点所有子树中的节点;
- 祖先节点:从树节点到该节点的路径上的节点;
- 节点的层次: 根节点为第一层,以此类推;
- 树的高度: 树中节点的最大层次;
- 有序树: 树中节点子树按次序从左向右安排, 次序不能改变;
- 无序树: 与有序树相反;
- 森林: 互不相交的树的集合.
树的性质
- 树的节点树为所有节点度数加1(加根节点);
- 度为m的树中第i层最多有m^(i-1)个节点;
- 高度为h的m次树至多(m^h-1)/(m-1)个节点;
- 具有n个节点的m次树的最小高度为logm( n(m-1) + 1 )向上取整;
二叉树
二叉树简介
二叉树是n(n>=0)个结点的有限集合,每一个结点中最多拥有一个左结点和一个右结点,并且没有多余的结点,如图所示:

二叉树的特点
根据二叉树的定义以及图示分析得出二叉树有以下特点:
- 每个结点最多有两颗子树,不存在度大于2的结点;
- 左子树和右子树的次序不能任意颠倒;
- 即使树中某结点只有一棵子树,也要区分它是左子树还是右子树;
二叉树的性质
二叉树具有以下几种特征
- 二叉树第i层上的结点数目最多为2{i-1} (i≥1);
- 深度为k的二叉树至多有(2{k}-1)(k≥1)个结点;
- 包含n个结点的二叉树的高度至少为log2 (n+1);
- 在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1;