什么是凸包?
这就是凸包:
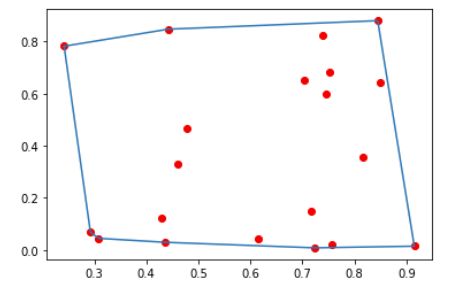
用什么方法找凸包?
- 葛立恒扫描法
由最底的一点A1开始, 计算它跟其他各点的连线和x轴的角度, 按小至大将这些角度排序, 称它们的对应点为A_2,A_3,\ldots,A_n. 这里的时间复杂度可达O(nlogn).
考虑最小的角度对应的点A3. 若由A2到A3的路径相对A1到A2的路径是向右转的(可以想象一个人沿A1走到A2, 他站在A2时, 是向哪边改变方向), 表示A3不可能是凸包上的一点, 考虑下一点由A2到A4的路径;否则就考虑A3到A4的路径是否向右转……直到回到A1.
这个算法的整体时间复杂度是O(nlogn), 注意每点只会被考虑一次, 而不像步进法中会考虑多次.
这个算法由葛立恒在1972年发明.它的缺点是不能推广到二维以上的情况.
- 包裹法(Jarvis步进法)
首先由一点必定在凸包的点开始, 例如最左的一点A1. 然后选择A2点使得所有点都在A1A2的右方, 这步骤的时间复杂度是O(n), 要比较所有点以A1为原点的极坐标角度.以A2为原点, 重复这个步骤, 依次找到A_3,A_4,\ldots,A_k,A_1.这总共有k步.因此, 时间复杂度为O(n^2).
- 单调链
将点按x坐标的值排列, 再按y坐标的值排列.
选择x坐标为最小值的点, 在这些点中找出y坐标的值最大和y坐标的值最小的点. 对于x坐标为最大值也是这样处理.将两组点中y坐标值较小的点连起. 在这条线段下的点, 找出它们之中y坐标值最大的点, 又在它们之间找x坐标值再最小和最大的点……如此类推. 时间复杂度是O(nlogn).
- 分治法
将点集X分成两个不相交子集. 求得两者的凸包后, 计算这两个凸包的凸包, 该凸包就是X的凸包.时间复杂度是O(nlogn).
- 快包法(Akl-Toussaint启发式)
选择最左、最右、最上、最下的点, 它们必组成一个凸四边形(或三角形).这个四边形内的点必定不在凸包上.然后将其余的点按最接近的边分成四部分, 再进行快包法(QuickHull).
当然, 我只是想使用葛立恒法找到凸包.
痛苦
首先要使用葛立恒法, 元素必须有序, 有两种方法可以选择, 一种是按照角度排序, 而另一种则是按照某一轴的坐标进行排序, 我毫不犹豫地选择了第二种.
用我之前的插入排序, 很容易接就得到了按照x轴坐标大小排好的点集, 然而我脑子根本不愿意动, 写了一个很诡异的代码跑不过之后就开始想去csdn和其他地方找找他们是怎么写的. 拜托, 你用的可是没人用的c#, 谁会来用这语言来复现这个算法!!! 醒醒吧!!!
然而, 我醒来之后已经三个小时过去了…
伪代码
凭借着我对我愚蠢的愤怒, 终于在几分钟内就理清了逻辑…

真代码
不得不说c#真好用
然而我连决定用什么数据结构都花了1个小时, 一会觉得Dictionary好, 一会封装成元组, 坐标最开始居然用的是两个List?!
- GACH
using System.Collections.Generic;
namespace Graham_Algrithm_on_Convex_Hall
{
public class GrahamsAlgronConvexHall
{
private static bool isLeft(double[] pt1, double[] pt2, double[] pt3) //使用叉积的定义
{
return (pt2[0] - pt1[0]) * (pt3[1] - pt1[1]) - (pt2[1] - pt1[1]) * (pt3[0] - pt1[0]) > 0;
}
/// <summary>
/// 以上下凸包葛立恒法返回凸包
/// </summary>
/// <param name="coord"></param>
/// <returns></returns>
public static List<double[]> GrahamConvexHall(List<double[]> coord)
{
List<double[]> newCoord = new List<double[]>();
//按x排序(插入排序)
for (int i = 1; i < coord.Count; i++)
{
double temp;
for (int j = i; j > 0 && coord[j][0] < coord[j - 1][0]; j--)
{
temp = coord[j][0];
coord[j][0] = coord[j - 1][0];
coord[j - 1][0] = temp;
temp = coord[j][1];
coord[j][1] = coord[j - 1][1];
coord[j - 1][1] = temp;
}
}
//上凸包
for (int i = 0; i < coord.Count; i++) {
if (newCoord.Count < 2) { //如果栈中元素小于两个则直接添加
newCoord.Add(coord[i]);
continue;
}
if (!isLeft(newCoord[newCoord.Count - 2], newCoord[newCoord.Count - 1], coord[i]))
newCoord.Add(coord[i]); //如果新点在栈里最新两点的右边入栈
else { //否则, 遍历之前所有栈中元素, 直到弹出所有在该点右边的线段
for (int j = newCoord.Count - 1; j>0 ; j--) {
if (isLeft(newCoord[j - 1], newCoord[j], coord[i]))
newCoord.RemoveAt(newCoord.Count - 1);
}
newCoord.Add(coord[i]);
}
}
int upConvex = newCoord.Count-1; //为了重复操作却不将最右边的元素重复入栈
//下凸包
for (int i = coord.Count-2; i >=0; i--) {
if (newCoord.Count - upConvex < 2) { //所以在这里减去upConvex
newCoord.Add(coord[i]);
continue;
}
if (!isLeft(newCoord[newCoord.Count - 2], newCoord[newCoord.Count - 1], coord[i]))
newCoord.Add(coord[i]);
else {
for (int j = newCoord.Count - 1; j > 0; j--) {
if (isLeft(newCoord[j - 1], newCoord[j], coord[i]))
newCoord.RemoveAt(newCoord.Count - 1);
}
newCoord.Add(coord[i]);
}
}
return newCoord;
}
}
}- 测试
using System;
using System.Collections.Generic;
namespace Graham_Algrithm_on_Convex_Hall
{
class Program
{
static void Main(string[] args)
{
Random random = new Random();
List<double[]> coordinates = new List<double[]> { };
List<double[]> newCoordinates = new List<double[]> { };
for (int i = 0; i < 20; i++)
{
coordinates.Add(new double[] { random.NextDouble(), random.NextDouble() });
}
foreach (var item in coordinates)
{
Console.Write(item[0] + ",");
}
Console.WriteLine();
foreach (var item in coordinates)
{
Console.Write(item[1] + ",");
}
newCoordinates = GrahamsAlgronConvexHall.GrahamConvexHall(coordinates);
Console.WriteLine();
Console.WriteLine();
foreach (var item in newCoordinates)
{
Console.Write(item[0] + ",");
}
Console.WriteLine();
foreach (var item in newCoordinates)
{
Console.Write(item[1] + ",");
}
Console.ReadLine();
}
}
}
结果
使用matplotlib输出图例:
import matplotlib.pyplot as plt
import numpy as np
plt.figure(figsize=(10, 10))
plt.plot([x坐标],[y坐标],
'ro')
plt.plot([凸包x坐标],[凸包x坐标])
plt.show()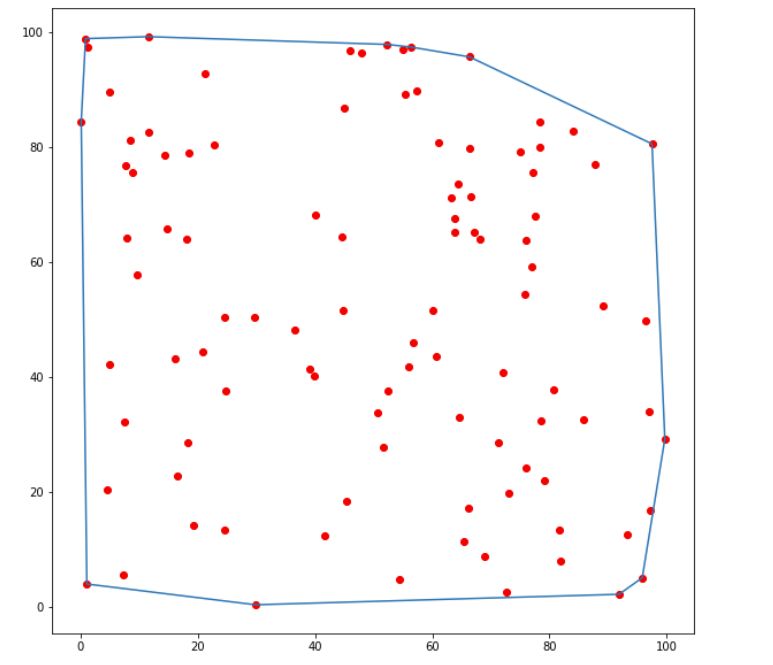
大功告成!!!
浪费我时间我好气哦!!!

