重新发明复数 篇七 复数域上的收敛性下篇
从收敛区间到收敛圆
神敲开实数的墙，创造了无上的圆。
我们在上一篇文章中讨论了f(x)=\frac{1}{x^2-1}的收敛性，我们可以看到，对于|f(x)|来说(一般来说，加绝对值不会对收敛区间有改变)，其收敛区间与爆破点的紧密联系:
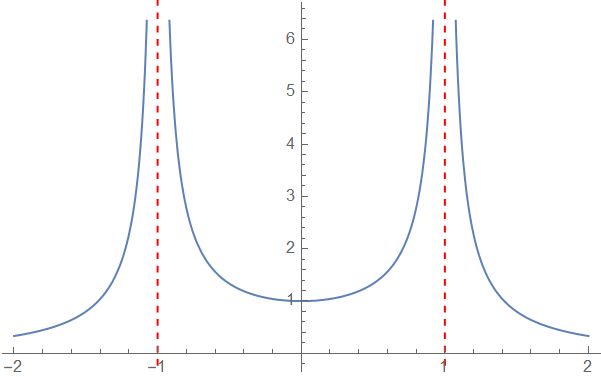
让我们在复数域上看看收敛区间是如何拓展的.
让我们直接对[……]
Somebody else looking in
神敲开实数的墙，创造了无上的圆。
我们在上一篇文章中讨论了f(x)=\frac{1}{x^2-1}的收敛性，我们可以看到，对于|f(x)|来说(一般来说，加绝对值不会对收敛区间有改变)，其收敛区间与爆破点的紧密联系:
让我们在复数域上看看收敛区间是如何拓展的.
让我们直接对[……]